Almost-period
A concept from the theory of almost-periodic functions (cf. Almost-periodic function); a generalization of the notion of a period. For a uniformly almost-periodic function  ,
, 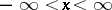 , a number
, a number  is called an
is called an  -almost-period of
-almost-period of 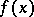 if for all
if for all  ,
,
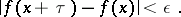 |
For generalized almost-periodic functions the concept of an almost-period is more complicated. For example, in the space  an
an  -almost-period
-almost-period  is defined by the inequality
is defined by the inequality
 |
where 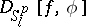 is the distance between
is the distance between 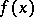 and
and 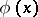 in the metric of
in the metric of 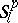 .
.
A set of almost-periods of a function 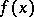 is said to be relatively dense if there is a number
is said to be relatively dense if there is a number 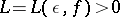 such that every interval
such that every interval 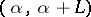 of the real line contains at least one number from this set. The concepts of uniformly almost-periodic functions and that of Stepanov almost-periodic functions may be defined by requiring the existence of relatively-dense sets of
of the real line contains at least one number from this set. The concepts of uniformly almost-periodic functions and that of Stepanov almost-periodic functions may be defined by requiring the existence of relatively-dense sets of  -almost-periods for these functions.
-almost-periods for these functions.
References
| [1] | B.M. Levitan, "Almost-periodic functions" , Moscow (1953) (In Russian) |
Comments
For the definition of 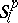 and its metric
and its metric 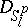 see Almost-periodic function. The Weyl, Besicovitch and Levitan almost-periodic functions can also be characterized in terms of
see Almost-periodic function. The Weyl, Besicovitch and Levitan almost-periodic functions can also be characterized in terms of 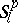
 -periods. These characterizations are more complicated. A good additional reference is [a1], especially Chapt. II.
-periods. These characterizations are more complicated. A good additional reference is [a1], especially Chapt. II.
References
| [a1] | A.S. Besicovitch, "Almost periodic functions" , Cambridge Univ. Press (1932) |
Almost-period. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Almost-period&oldid=32494