Algebraically closed field
A field  in which any polynomial of non-zero degree over
in which any polynomial of non-zero degree over  has at least one root. In fact, it follows that for an algebraically closed field
has at least one root. In fact, it follows that for an algebraically closed field 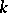 each polynomial of degree
each polynomial of degree  over
over  has exactly
has exactly  roots in
roots in  , i.e. each irreducible polynomial from the ring of polynomials
, i.e. each irreducible polynomial from the ring of polynomials 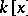 is of degree one. A field
is of degree one. A field  is algebraically closed if and only if it has no proper algebraic extension (cf. Extension of a field). For any field
is algebraically closed if and only if it has no proper algebraic extension (cf. Extension of a field). For any field  , there exists a unique (up to isomorphism) algebraic extension of
, there exists a unique (up to isomorphism) algebraic extension of 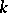 that is algebraically closed; it is called the algebraic closure of
that is algebraically closed; it is called the algebraic closure of 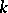 and is usually denoted by
and is usually denoted by  . Any algebraically closed field containing
. Any algebraically closed field containing  contains a subfield isomorphic to
contains a subfield isomorphic to  .
.
The field of complex numbers is the algebraic closure of the field of real numbers. This is the fundamental theorem of algebra (cf. Algebra, fundamental theorem of).
References
| [1] | O. Zariski, P. Samuel, "Commutative algebra" , 1 , Springer (1975) |
| [2] | S. Lang, "Algebra" , Addison-Wesley (1974) |
Algebraically closed field. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Algebraically_closed_field&oldid=11228