Algebraic systems, quasi-variety of
A class of algebraic systems ( -systems) axiomatized by special formulas of a first-order logical language, called quasi-identities or conditional identities, of the form
-systems) axiomatized by special formulas of a first-order logical language, called quasi-identities or conditional identities, of the form
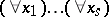 |
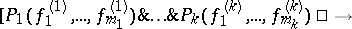 |
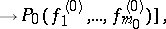 |
where 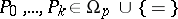 , and
, and  are terms of the signature
are terms of the signature  in the object variables
in the object variables  . By virtue of Mal'tsev's theorem [1] a quasi-variety
. By virtue of Mal'tsev's theorem [1] a quasi-variety 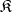 of algebraic systems of signature
of algebraic systems of signature  can also be defined as an abstract class of
can also be defined as an abstract class of  -systems containing the unit
-systems containing the unit  -system
-system 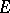 , and which is closed with respect to subsystems and filtered products [1], [2]. An axiomatizable class of
, and which is closed with respect to subsystems and filtered products [1], [2]. An axiomatizable class of  -systems is a quasi-variety if and only if it contains the unit
-systems is a quasi-variety if and only if it contains the unit  -system
-system 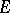 and is closed with respect to subsystems and Cartesian products. If
and is closed with respect to subsystems and Cartesian products. If 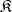 is a quasi-variety of signature
is a quasi-variety of signature  , the subclass
, the subclass 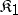 of systems of
of systems of 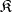 that are isomorphically imbeddable into suitable systems of some quasi-variety
that are isomorphically imbeddable into suitable systems of some quasi-variety 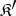 with signature
with signature 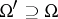 , is itself a quasi-variety. Thus, the class of semi-groups imbeddable into groups is a quasi-variety; the class of associative rings without zero divisors imbeddable into associative skew-fields is also a quasi-variety.
, is itself a quasi-variety. Thus, the class of semi-groups imbeddable into groups is a quasi-variety; the class of associative rings without zero divisors imbeddable into associative skew-fields is also a quasi-variety.
A quasi-variety 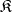 of signature
of signature  is called finitely definable (or, is said to have a finite basis of quasi-identities) if there exists a finite set
is called finitely definable (or, is said to have a finite basis of quasi-identities) if there exists a finite set 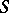 of quasi-identities of
of quasi-identities of  such that
such that 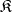 consists of only those
consists of only those  -systems in which all the formulas from the set
-systems in which all the formulas from the set 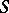 are true. For instance, the quasi-variety of all semi-groups with cancellation is defined by the two quasi-identities
are true. For instance, the quasi-variety of all semi-groups with cancellation is defined by the two quasi-identities
 |
and is therefore finitely definable. On the other hand, the quasi-variety of semi-groups imbeddable into groups has no finite basis of quasi-identities [1], [2].
Let 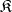 be an arbitrary (not necessarily abstract) class of
be an arbitrary (not necessarily abstract) class of  -systems; the smallest quasi-variety containing
-systems; the smallest quasi-variety containing 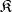 is said to be the implicative closure of the class
is said to be the implicative closure of the class 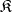 . It consists of subsystems of isomorphic copies of filtered products of
. It consists of subsystems of isomorphic copies of filtered products of  -systems of the class
-systems of the class 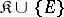 , where
, where 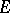 is the unit
is the unit  -system. If
-system. If 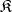 is the implicative closure of a class
is the implicative closure of a class 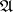 of
of  -systems,
-systems, 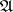 is called a generating class of the quasi-variety
is called a generating class of the quasi-variety 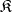 . A quasi-variety
. A quasi-variety 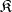 is generated by one system if and only if for any two systems
is generated by one system if and only if for any two systems 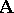 ,
, 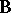 of
of 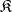 there exists in the class
there exists in the class 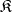 a system
a system 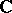 containing subsystems isomorphic to
containing subsystems isomorphic to 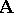 and
and 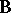 [1]. Any quasi-variety
[1]. Any quasi-variety 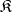 containing systems other than one-element systems has free systems of any rank, which are at the same time free systems in the equational closure of the class
containing systems other than one-element systems has free systems of any rank, which are at the same time free systems in the equational closure of the class 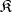 . The quasi-varieties of
. The quasi-varieties of  -systems contained in some given quasi-variety
-systems contained in some given quasi-variety 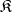 of signature
of signature  constitute a complete lattice with respect to set-theoretic inclusion. The atoms of the lattice of all quasi-varieties of signature
constitute a complete lattice with respect to set-theoretic inclusion. The atoms of the lattice of all quasi-varieties of signature  are called minimal quasi-varieties of
are called minimal quasi-varieties of  . A minimal quasi-variety
. A minimal quasi-variety 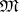 is generated by any one of its non-unit systems. Every quasi-variety with a non-unit system contains at least one minimal quasi-variety. If
is generated by any one of its non-unit systems. Every quasi-variety with a non-unit system contains at least one minimal quasi-variety. If 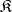 is a quasi-variety of
is a quasi-variety of  -systems of finite signature
-systems of finite signature  , all its sub-quasi-varieties constitute a groupoid with respect to the Mal'tsev
, all its sub-quasi-varieties constitute a groupoid with respect to the Mal'tsev 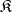 -multiplication [3].
-multiplication [3].
References
| [1] | A.I. Mal'tsev, "Algebraic systems" , Springer (1973) (Translated from Russian) |
| [2] | P.M. Cohn, "Universal algebra" , Reidel (1981) |
| [3] | A.I. Mal'tsev, "Multiplication of classes of algebraic systems" Siberian Math. J. , 8 : 2 (1967) pp. 254–267 Sibirsk Mat. Zh. , 8 : 2 (1967) pp. 346–365 |
Comments
In the Western literature, quasi-identities are commonly called Horn sentences (cf. [a1]). For a categorical treatment of quasi-varieties, see [a3]; for their finitary analogue, see [a2]. Mal'tsev's article [a3] may also be found in [a4] as Chapt. 32.
References
| [a1] | A. Horn, "On sentences which are true of direct unions of algebras" J. Symbolic Logic , 16 (1951) pp. 14–21 |
| [a2] | J.R. Isbell, "General functional semantics, I" Amer. J. Math. , 94 (1972) pp. 535–596 |
| [a3] | O. Keane, "Abstract Horn theories" F.W. Lawvere (ed.) C. Maurer (ed.) C. Wraith (ed.) , Model theory and topoi , Lect. notes in math. , 445 , Springer (1975) pp. 15–50 |
| [a4] | A.I. [A.I. Mal'tsev] Mal'cev, , The metamathematics of algebraic systems. Collected papers: 1936 - 1967 , North-Holland (1971) |
Algebraic systems, quasi-variety of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Algebraic_systems,_quasi-variety_of&oldid=19285