Algebraic logic
Algebraic logic can be divided into two major parts: abstract (or universal) algebraic logic and "concrete" algebraic logic (or algebras of relations of various ranks). Both are discussed below.
Abstract algebraic logic.
This branch of algebraic logic is built around a duality theory which associates, roughly speaking, quasi-varieties of algebras to logical systems (logics for short) and vice versa. After the duality theory is elaborated, characterization theorems follow, characterizing distinguished logical properties of a logic 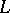 in terms of natural algebraic properties of the algebraic counterpart
in terms of natural algebraic properties of the algebraic counterpart  of
of 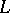 .
.
A logic is, usually, a tuple
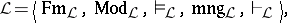 |
where 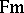 is the set of formulas of
is the set of formulas of 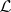 ,
, 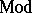 is the class of models of
is the class of models of 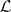 ,
, 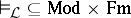 is the validity relation,
is the validity relation, 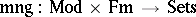 is the semantical meaning (or denotation) function of
is the semantical meaning (or denotation) function of 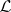 , and
, and  is the syntactical provability relation of
is the syntactical provability relation of 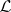 .
.
More generally, a general logic consists of a class 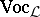 of vocabularies and then to each vocabulary
of vocabularies and then to each vocabulary 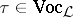 ,
,  associates a logic, i.e. a
associates a logic, i.e. a  -tuple
-tuple  as indicated above. As an example, first-order logic is a general logic in the sense that to any collection of predicate symbols it associates a concrete first-order language built up from those predicate symbols (i.e. that vocabulary; cf. also Mathematical logic).
as indicated above. As an example, first-order logic is a general logic in the sense that to any collection of predicate symbols it associates a concrete first-order language built up from those predicate symbols (i.e. that vocabulary; cf. also Mathematical logic).
Of course, there are some conditions which logics and general logics have to satisfy, otherwise any "crazy" odd  -tuple would count as a logic, which one wants to avoid. (E.g., one assumes that if
-tuple would count as a logic, which one wants to avoid. (E.g., one assumes that if 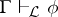 and
and 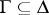 , then
, then 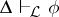 , for
, for 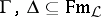 .) For such conditions on logics and general logics, see [a4], [a27], [a24], or, for the case of logics without semantics (i.e. without
.) For such conditions on logics and general logics, see [a4], [a27], [a24], or, for the case of logics without semantics (i.e. without 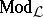 ), [a7]. These conditions go back to pioneering papers of A. Tarski, cf. [a34].
), [a7]. These conditions go back to pioneering papers of A. Tarski, cf. [a34].
To each logic and general logic there is associated a set 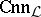 of logical connectives, specified in such a way that
of logical connectives, specified in such a way that 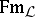 or
or 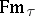 becomes an absolutely free algebra (cf. also Free algebra) generated by the atomic formulas of
becomes an absolutely free algebra (cf. also Free algebra) generated by the atomic formulas of  and
and 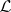 and using
and using 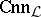 as algebraic operations. Hence one can view
as algebraic operations. Hence one can view 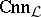 as the similarity type of the algebras
as the similarity type of the algebras 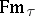 . Using the algebras
. Using the algebras 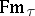 and the provability relation
and the provability relation 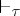 , one can associate a class
, one can associate a class 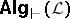 of algebras to
of algebras to 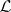 . Each of these algebras corresponds to a syntactical theory of
. Each of these algebras corresponds to a syntactical theory of 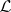 . Using
. Using 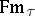 together with
together with  and
and 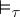 , one can associate a second class
, one can associate a second class 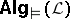 of algebras to
of algebras to 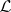 .
. 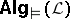 represents semantical aspects of
represents semantical aspects of  , e.g. each model
, e.g. each model 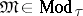 corresponds to an algebra in
corresponds to an algebra in 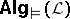 . Often, the members of
. Often, the members of 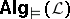 are called representable algebras or meaning algebras of
are called representable algebras or meaning algebras of 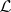 . Under mild conditions on
. Under mild conditions on 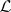 , one can prove that
, one can prove that 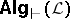 is a quasi-variety and that
is a quasi-variety and that 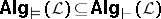 . If the logic
. If the logic  is complete, then
is complete, then 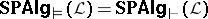 , cf. e.g. [a4].
, cf. e.g. [a4].
Examples.
If 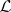 is propositional logic (cf. also Mathematical logic; Propositional calculus), then
is propositional logic (cf. also Mathematical logic; Propositional calculus), then 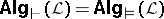 is the class
is the class 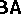 of Boolean algebras (cf. Boolean algebra). Let
of Boolean algebras (cf. Boolean algebra). Let 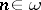 . For the
. For the  -variable fragment
-variable fragment 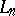 of first-order logic,
of first-order logic, 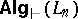 is the class
is the class 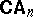 of cylindric algebras of dimension
of cylindric algebras of dimension  , while
, while 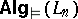 is the class
is the class 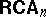 of representable cylindric algebras. For a certain variant
of representable cylindric algebras. For a certain variant 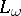 of first-order logic,
of first-order logic, 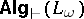 is the class
is the class 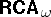 of representable
of representable 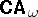 s.
s. 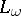 is called the full restricted first-order language in [a11], Vol. II, cf. also [a4], § 6, and [a7], Appendix C. For the algebraic counterparts of other logics (as well as other versions of first-order logic), see [a4].
is called the full restricted first-order language in [a11], Vol. II, cf. also [a4], § 6, and [a7], Appendix C. For the algebraic counterparts of other logics (as well as other versions of first-order logic), see [a4].
Now, take the logic 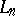 as an example. The algebraic counterparts of theories of
as an example. The algebraic counterparts of theories of 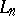 are exactly the algebras in
are exactly the algebras in 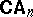 and the interpretations between theories correspond exactly to the homomorphisms between
and the interpretations between theories correspond exactly to the homomorphisms between 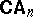 s. Further, axiomatizable classes of models of
s. Further, axiomatizable classes of models of 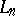 correspond to
correspond to  s and (semantic) interpretations between such classes of models correspond to special homomorphisms, called base-homomorphisms, between
s and (semantic) interpretations between such classes of models correspond to special homomorphisms, called base-homomorphisms, between 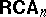 s, cf. [a11], Vol. II, p. 170. Individual models of
s, cf. [a11], Vol. II, p. 170. Individual models of 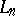 correspond to simple
correspond to simple  s and elementary equivalence of models corresponds to isomorphism of
s and elementary equivalence of models corresponds to isomorphism of 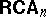 s. The elements of an
s. The elements of an 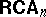 corresponding to a model
corresponding to a model 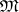 are best thought of as the relations definable in
are best thought of as the relations definable in  .
.
Of the duality theory between logics and their algebraic counterparts only the translation
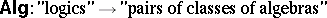 |
was discussed above. The other direction can also be elaborated (and then a two-sided duality like Stone duality between 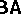 s and certain topological spaces can occur; cf. also Stone space); see [a7], p.21, for more on such a two-sided duality between logics and quasi-varieties of algebras.
s and certain topological spaces can occur; cf. also Stone space); see [a7], p.21, for more on such a two-sided duality between logics and quasi-varieties of algebras.
Some equivalence theorems.
Using the duality theory outlined above, logical properties of 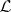 can be characterized by algebraic properties of
can be characterized by algebraic properties of 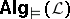 ,
, 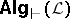 (under some mild assumptions on
(under some mild assumptions on 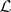 ). E.g. the deduction property of
). E.g. the deduction property of 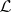 is equivalent with
is equivalent with  having equationally definable principal congruences. The Beth definability property for
having equationally definable principal congruences. The Beth definability property for 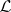 is equivalent with surjectiveness of all epimorphisms in
is equivalent with surjectiveness of all epimorphisms in 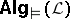 . The various definability properties (weak Beth, local Beth, etc.) and interpolation properties are equivalent with distinguished versions of the amalgamation property and surjectiveness of epimorphisms, respectively, in
. The various definability properties (weak Beth, local Beth, etc.) and interpolation properties are equivalent with distinguished versions of the amalgamation property and surjectiveness of epimorphisms, respectively, in 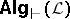 or
or 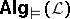 . A kind of completeness theorem for
. A kind of completeness theorem for 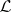 is equivalent with finite axiomatizability of
is equivalent with finite axiomatizability of 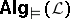 . Compactness of
. Compactness of 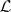 is equivalent with
is equivalent with 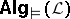 being closed under ultraproducts. The above (and further) equivalence theorems are elaborated in e.g. [a4]. Further such results can be found in e.g. [a11], [a7], [a22], [a23], [a31], [a14], [a21], [a19], work of J. Czelakowski, L. Maksimova, and the references in [a35]. A duality theory for algebraic logic is in [a8]. An overview of duality theories is in [a2], Chap. 6.
being closed under ultraproducts. The above (and further) equivalence theorems are elaborated in e.g. [a4]. Further such results can be found in e.g. [a11], [a7], [a22], [a23], [a31], [a14], [a21], [a19], work of J. Czelakowski, L. Maksimova, and the references in [a35]. A duality theory for algebraic logic is in [a8]. An overview of duality theories is in [a2], Chap. 6.
Concrete algebraic logic.
This branch investigates classes of algebras that arise in the algebraization of the most frequently used logics. Below, attention is restricted to algebras of classical quantifier logics, algebras of the finite variable fragments 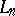 of these logics, relativized versions of these logics, e.g. the guarded fragment, and logics of the dynamic trend, whose algebras are relation algebras or relativized relation algebras. See also Abstract algebraic logic. The objective is to "algebraize" logics which extend classical propositional logic. The algebras of this propositional logic are Boolean algebras (cf. also Boolean algebra). Boolean algebras are natural algebras of unary relations. One expects the algebras of the extended logics to be extensions of Boolean algebras to algebras of relations of higher ranks. The elements of a Boolean algebra are sets of points; one expects the elements of the new algebras to be sets of sequences (since relations are sets of sequences).
of these logics, relativized versions of these logics, e.g. the guarded fragment, and logics of the dynamic trend, whose algebras are relation algebras or relativized relation algebras. See also Abstract algebraic logic. The objective is to "algebraize" logics which extend classical propositional logic. The algebras of this propositional logic are Boolean algebras (cf. also Boolean algebra). Boolean algebras are natural algebras of unary relations. One expects the algebras of the extended logics to be extensions of Boolean algebras to algebras of relations of higher ranks. The elements of a Boolean algebra are sets of points; one expects the elements of the new algebras to be sets of sequences (since relations are sets of sequences).
 -ary representable cylindric algebras (
-ary representable cylindric algebras (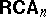 s) are algebras of
s) are algebras of  -ary relations. They correspond to the
-ary relations. They correspond to the  -variable fragment
-variable fragment 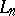 of first-order logic. The new operations are cylindrifications
of first-order logic. The new operations are cylindrifications 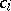 (
(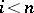 ). If
). If  is a relation defined by a formula
is a relation defined by a formula 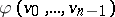 , then
, then 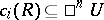 is the relation defined by the formula
is the relation defined by the formula 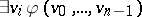 . (To be precise, one should write
. (To be precise, one should write 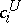 for
for 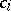 .) Assume
.) Assume 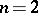 ,
, 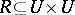 . Then
. Then 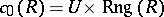 and
and 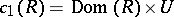 . This shows that
. This shows that 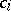 is a natural and simple operation on
is a natural and simple operation on  -ary relations: it simply abstracts from the
-ary relations: it simply abstracts from the 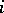 th argument of the relation. Let
th argument of the relation. Let 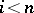 ,
,  . Then
. Then
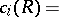 |
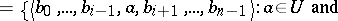 |
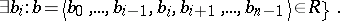 |
In other words, if 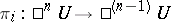 is the canonical projection along the
is the canonical projection along the 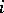 th factor, then
th factor, then
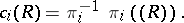 |
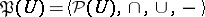 denotes the Boolean algebra of all subsets of
denotes the Boolean algebra of all subsets of 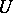 . The algebra of
. The algebra of  -ary relations over
-ary relations over 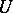 is
is
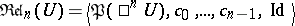 |
where the constant operation 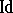 is the
is the  -ary identity relation,
-ary identity relation, 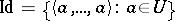 over
over 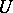 . E.g. the smallest subalgebra of
. E.g. the smallest subalgebra of 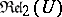 has
has 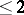 atoms, while that of
atoms, while that of 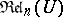 has
has 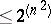 atoms. The class
atoms. The class 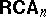 of
of  -ary representable cylindric algebras is defined as
-ary representable cylindric algebras is defined as
 |
where 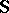 and
and 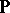 are the operators on classes of algebras corresponding to taking isomorphs of subalgebras and direct products, respectively.
are the operators on classes of algebras corresponding to taking isomorphs of subalgebras and direct products, respectively.
Let 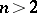 . Then
. Then 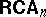 is a discriminator variety, with an undecidable but recursively enumerable equational theory.
is a discriminator variety, with an undecidable but recursively enumerable equational theory. 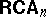 is not finitely axiomatizable, fails to have almost any form of the amalgamation property and has non-surjective epimorphisms. Almost all of these theorems remain true if one throws away the constant
is not finitely axiomatizable, fails to have almost any form of the amalgamation property and has non-surjective epimorphisms. Almost all of these theorems remain true if one throws away the constant 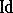 (from
(from 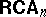 ) and closes up under
) and closes up under 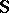 to make it a universally axiomatizable class. These properties imply theorems about
to make it a universally axiomatizable class. These properties imply theorems about 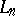 via the duality theory between logics and classes of algebras elaborated in abstract algebraic logic. Further, usual set theory can be built up in
via the duality theory between logics and classes of algebras elaborated in abstract algebraic logic. Further, usual set theory can be built up in 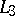 (and even in the equational theory of
(and even in the equational theory of 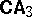 ). Hence
). Hence 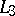 (and
(and 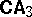 ) have the "Gödel incompleteness property" , cf. [a28] and also Gödel incompleteness theorem.
) have the "Gödel incompleteness property" , cf. [a28] and also Gödel incompleteness theorem.
For first-order logic 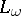 with infinitely many variables (cf. e.g. [a7], Appendix C), the algebraic counterpart is
with infinitely many variables (cf. e.g. [a7], Appendix C), the algebraic counterpart is 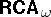 (algebras of
(algebras of 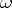 -ary relations). To generalize
-ary relations). To generalize 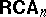 to
to 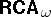 , one needs only a single non-trivial step: one has to brake up the single constant
, one needs only a single non-trivial step: one has to brake up the single constant 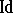 to a set of constants
to a set of constants 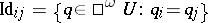 , with
, with 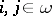 . Now
. Now
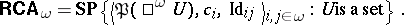 |
The definition of 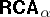 with
with 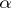 an arbitrary ordinal number is practically the same.
an arbitrary ordinal number is practically the same. 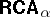 is an arithmetical variety, not axiomatizable by any set
is an arithmetical variety, not axiomatizable by any set 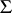 of formulas involving only finitely many individual variables. Most of the theorems about
of formulas involving only finitely many individual variables. Most of the theorems about  mentioned above carry over to
mentioned above carry over to 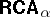 .
.
The greatest element of a "generic" 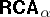 was required to be a Cartesian space
was required to be a Cartesian space 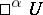 . If one removes this condition and replaces
. If one removes this condition and replaces 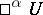 with an arbitrary
with an arbitrary 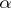 -ary relation
-ary relation 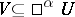 in the definition, one obtains the important generalization
in the definition, one obtains the important generalization 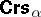 of
of 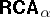 . Many of the negative properties of
. Many of the negative properties of 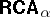 disappear in
disappear in 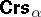 . E.g., the equational theory is decidable, is a variety generated by its finite members, enjoys the super-amalgamation property (hence the strong amalgamation property (SAP), too), etc. Logic applications of
. E.g., the equational theory is decidable, is a variety generated by its finite members, enjoys the super-amalgamation property (hence the strong amalgamation property (SAP), too), etc. Logic applications of 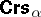 abound, cf. e.g. [a5], [a37], [a10], [a26], [a18].
abound, cf. e.g. [a5], [a37], [a10], [a26], [a18].
Since 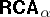 is not finite schema axiomatizable, a finitely schematizable approximation
is not finite schema axiomatizable, a finitely schematizable approximation 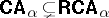 was introduced by Tarski. There are theorems to the effect that
was introduced by Tarski. There are theorems to the effect that 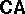 s approximate
s approximate 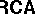 s well, cf. [a11], Vol. II, §3.2, [a25].
s well, cf. [a11], Vol. II, §3.2, [a25].
The above illustrates the flavour of the theory of algebras of relations; important kinds of algebras not mentioned include relation algebras and quasi-polyadic algebras, cf. e.g. [a11], Vol. II, [a33], [a9], [a4], [a30], [a29], [a13]. The theory of the latter two is analogous with that of 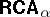 s. Common generalizations of
s. Common generalizations of 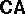 s,
s, 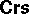 s, relation algebras, polycyclic algebras, and their variants is the important class of Boolean algebras with operators, cf., e.g., [a16], [a8], [a15], [a34], [a1], [a17]. For category-theoretic approaches, see [a4] and the references therein.
s, relation algebras, polycyclic algebras, and their variants is the important class of Boolean algebras with operators, cf., e.g., [a16], [a8], [a15], [a34], [a1], [a17]. For category-theoretic approaches, see [a4] and the references therein.
There are many open problems in this area (cf. e.g. [a30], [a12], [a3], pp. 727–745, [a32]). To mention one (open as of 2000): is there a variety 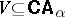 having the strong amalgamation property (SAP) but not the super-amalgamation property?
having the strong amalgamation property (SAP) but not the super-amalgamation property?
Application areas of algebraic logic range from logic and linguistics through cognitive science, to even relativity theory, cf., e.g., the work of the Amsterdam school [a6], [a36], [a20], [a37], and [a2].
This work was supported by the Hungarian National Foundation for Scientific Research T30314, T35192.
References
| [a1] | H. Andréka, S. Givant, Sz. Mikulás, I. Németi, A. Simon, "Notions of density that imply representability in algebraic logic" Ann. Pure Appl. Logic , 91 (1998) pp. 93–190 |
| [a2] | H. Andréka, J.X. Madarász, I. Németi, "On the logical structure of relativity theories" , A. Rényi Inst. Math. (2001) (www.math-inst.hu/pub/algebraic-logic) |
| [a3] | "Algebraic logic (Proc. Conf. Budapest 1988)" H. Andréka (ed.) J.D. Monk (ed.) I. Németi (ed.) , Colloq. Math. Soc. J. Bolyai , 54 , North-Holland (1991) |
| [a4] | H. Andréka, I. Németi, I. Sain, "Algebraic logic" , Handbook of Philosophical Logic , 1 , Kluwer Acad. Publ. (2001) (www.math-inst.hu/pub/algebraic-logic) |
| [a5] | H. Andréka, J. van Benthem, I. Németi, "Modal languages and bounded fragments of predicate logic" J. Philos. Logic , 27 (1998) pp. 217–274 |
| [a6] | "Handbook of Logic and Language" J. van Benthem (ed.) A. ter Meulen (ed.) , Elsevier (1997) |
| [a7] | W.J. Blok, D.L. Pigozzi, "Algebraizable logics" Memoirs Amer. Math. Soc. , 77 : 396 (1989) |
| [a8] | R. Goldblatt, "Algebraic polymodal logic: A survey" Logic J. IGPL , 8 : 4 (2000) pp. 393–450 |
| [a9] | R. Hirsch, I. Hodkinson, "Relation algebras by games" , Kluwer Acad. Publ. (to appear) |
| [a10] | E. Hoogland, M. Marx, "Interpolation in guarded fragments" Studia Logica (2000) |
| [a11] | L. Henkin, J.D. Monk, A. Tarski, "Cylindric algebras" , I—II , North-Holland (1971/85) |
| [a12] | L. Henkin, J.D. Monk, A. Tarski, H. Andréka, I. Németi, "Cylindric set algebras" , Lecture Notes in Math. , 883 , Springer (1981) |
| [a13] | "Handbook on the heart of algebra" R.A. Mikhalev (ed.) G.F. Pilz (ed.) , Kluwer Acad. Publ. (to appear) |
| [a14] | E. Hoogland, "Algebraic characterizations of various Beth definability properties" Studia Logica , 65 : 1 (2000) pp. 91–112 |
| [a15] | P. Jipsen, B. Jónsson, J. Rafter, "Adjoining units to residuated Boolean algebras" Algebra Univ. , 34 : 2 (1995) pp. 118–127 |
| [a16] | B. Jónsson, A. Tarski, "Boolean algebras with operators" , Alfred Tarski Collected Papers , 3 , Birkhäuser (1986) |
| [a17] | Á. Kurucz, "Decision problems in algebraic logic" PhD Diss., Budapest (1997) (www.math-inst.hu/pub/algebraic-logic) |
| [a18] | "Arrow logic and multi-modal logic" M. Marx (ed.) L. Pólos (ed.) M. Masuch (ed.) , CSLI Publ. (1996) |
| [a19] | J.X. Madarász, T. Sayed-Ahmed, "Amalgamation, interpolation and epimorphisms, solutions to all problems of Pigozzi's paper, and some more" A. Rényi Inst. Math. (2001) |
| [a20] | M. Marx, Y. Venema, "Multi-dimensional modal logic" , Kluwer Acad. Publ. (1997) |
| [a21] | J.X. Madarász, "Surjectiveness of epimorphisms in varieties of algebraic logic" Preprint A. Rényi Inst. Math. (2000) |
| [a22] | J.X. Madarász, "Interpolation and amalgamation: Pushing the limits (I)" Studia Logica , 61 : 3 (1998) pp. 311–345 |
| [a23] | J.X. Madarász, "Interpolation and amalgamation: Pushing the limits (II)" Studia Logica , 62 : 1 (1999) pp. 1–19 |
| [a24] | N. Marti-Oliet, J. Meseguer, "General logics and logical frameworks" D.M. Gabbay (ed.) , What is a Logical System , Clarendon Press (1994) pp. 355–392 |
| [a25] | J.D. Monk, "An introduction to cylindric set algebras" Logic J. IGPL , 8 : 4 (2000) pp. 451–506 |
| [a26] | I. Németi, "Fine-structure analysis of first order logic" M. Marx (ed.) L. Pólos (ed.) M. Masuch (ed.) , Arrow Logic and Multi-Modal Logic , CSLI Publ. (1996) pp. 221–247 |
| [a27] | I. Németi, H. Andréka, "General algebraic logic: A perspective on what is logic" D.M. Gabbay (ed.) , What is a Logical System , Clarendon Press (1994) pp. 393–444 |
| [a28] | I. Németi, "Logic with three variables has Gödel's incompleteness property—thus free cylindric algebras are not atomic" Manuscript Math. Inst. Hungar. Acad. Sci., Budapest (1986) |
| [a29] | "Special issue on Algebraic Logic" I. Németi (ed.) I. Sain (ed.) Logic J. IGPL , 8 : 4 (2000) (I. Nemeti and I. Sain) |
| [a30] | I. Németi, "Algebraization of quantifier logics, an introductory overview" Studia Logica , 50 : 3/4 (1991) pp. 485–570 (Special issue devoted to Algebraic Logic, eds.: W.J. Blok and D.L. Pigozzi. This is a preliminary, short version (without proofs, etc.) of www.math-inst.hu/pub/algebraic-logic) |
| [a31] | D.L. Pigozzi, "Amalgamation, congruence-extensions, and interpolation properties in algebras" Algebra Univ. , 1 : 3 (1972) pp. 269–349 |
| [a32] | A. Simon, "Non-representable algebras of relations" PhD Diss., Budapest (1997) (www.math-inst.hu/pub/algebraic-logic) |
| [a33] | A. Tarski, S. Givant, "A formalization of set theory without variables" , Colloq. Publ. , 41 , Amer. Math. Soc. (1987) |
| [a34] | S.R. Givant (ed.) R.N. McKenzie (ed.) , Alfred Tarski: Collected Works , 1–4 , Birkhäuser (1986) (S.R. Givant and R.N. McKenzie) |
| [a35] | "Special issue on abstract algebraic logic" J.M. Font (ed.) R. Jansana (ed.) D. Pigozzi (ed.) Studia Logica , 65 : 1 (2000) (J.M. Font and R. Jansana and D. Pigozzi) |
| [a36] | J. van Benthem, "Language in action (categories, lambdas and dynamic logic)" , Studies in Logic , 130 , North-Holland (1991) |
| [a37] | J.A.F.K. van Benthem, "Exploring logical dynamics" , Studies in Logic, Language and Information , CSLI Publ. (1996) |
Algebraic logic. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Algebraic_logic&oldid=16656