Algebraic group of transformations
An algebraic group  acting regularly on an algebraic variety
acting regularly on an algebraic variety  . More precisely, it is a triplet
. More precisely, it is a triplet  where
where  (
(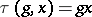 ) is a morphism of algebraic varieties satisfying the conditions:
) is a morphism of algebraic varieties satisfying the conditions: 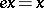 ,
, 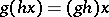 for all
for all  and
and  (where
(where  is the unit of
is the unit of 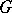 ). If
). If 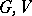 and
and  are defined over a field
are defined over a field 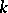 , then
, then  is called an algebraic group of
is called an algebraic group of  -transformations. For instance,
-transformations. For instance, 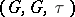 , where
, where  is the adjoint action or an action by shifts, is an algebraic group of transformations. If
is the adjoint action or an action by shifts, is an algebraic group of transformations. If 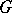 is an algebraic subgroup in
is an algebraic subgroup in 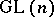 and
and  is its natural action on the affine space
is its natural action on the affine space  , then
, then 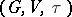 is an algebraic group of transformations. For each point
is an algebraic group of transformations. For each point 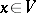 one denotes by
one denotes by 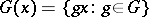 the orbit of
the orbit of  , and by
, and by  the stabilizer of
the stabilizer of  . The orbit
. The orbit 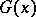 need not necessarily be closed in
need not necessarily be closed in  , but closed orbits exist always, e.g. orbits of minimal dimension are closed. An algebraic group of transformations is sometimes understood to mean a group
, but closed orbits exist always, e.g. orbits of minimal dimension are closed. An algebraic group of transformations is sometimes understood to mean a group 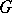 which is acting rationally (but not necessarily regularly) on an algebraic variety
which is acting rationally (but not necessarily regularly) on an algebraic variety  (this means that
(this means that 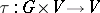 is a rational mapping, and the above properties of
is a rational mapping, and the above properties of  are valid for ordinary points). It was shown by A. Weil [3] that there always exists a variety
are valid for ordinary points). It was shown by A. Weil [3] that there always exists a variety 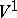 , birationally isomorphic to
, birationally isomorphic to  , and such that the action of
, and such that the action of  on
on  induced by the rational action of
induced by the rational action of 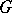 on
on 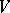 is regular. The problem of describing the orbits, stabilizers, fields of invariant rational functions (cf. Invariants, theory of), and of constructing quotient varieties are fundamental in the theory of algebraic groups of transformations and have numerous applications.
is regular. The problem of describing the orbits, stabilizers, fields of invariant rational functions (cf. Invariants, theory of), and of constructing quotient varieties are fundamental in the theory of algebraic groups of transformations and have numerous applications.
References
| [1] | A. Borel, "Linear algebraic groups" , Benjamin (1969) |
| [2a] | J.A. Dieudonné, "Invariant theory: old and new" , Acad. Press (1971) |
| [2b] | D. Mumford, "Geometric invariant theory" , Springer (1965) |
| [2c] | D. Mumford, "Projective invariants of projective structures and applications" , Proc. Internat. Congress mathematicians (Stockholm, 1962) , Inst. Mittag-Leffler (1963) pp. 526–530 |
| [2d] | C.S. Seshadri, "Quotient spaces modulo reductive groupes and applications to moduli of vector bundles on algebraic curves" , Proc. Internat. Congress Mathematicians (Nice, 1970) , 1 , Gauthier-Villars (1971) pp. 479–482 |
| [3] | A. Weil, "On algebraic groups and homogeneous spaces" Amer. J. Math. , 77 : 2 (1955) pp. 355–391 |
Comments
The notion in question is also called an algebraic transformation space.
Algebraic group of transformations. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Algebraic_group_of_transformations&oldid=13276