Algebraic branch point
algebraic singular point
An isolated branch point  of finite order of an analytic function
of finite order of an analytic function  , having the property that the limit
, having the property that the limit  exists for any regular element of continuation of
exists for any regular element of continuation of  in a domain for which
in a domain for which  is a boundary point. More exactly, a singular point
is a boundary point. More exactly, a singular point  in the complex
in the complex  -plane for the complete analytic function
-plane for the complete analytic function  , under continuation of some regular element
, under continuation of some regular element  of this function with centre
of this function with centre  along paths passing through
along paths passing through  , is called an algebraic branch point if it fulfills the following conditions: 1) There exists a positive number
, is called an algebraic branch point if it fulfills the following conditions: 1) There exists a positive number  such that the element
such that the element 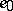 may be extended along an arbitrary continuous curve lying in the annulus
may be extended along an arbitrary continuous curve lying in the annulus  ; 2) there exists a positive integer
; 2) there exists a positive integer  such that if
such that if 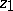 is an arbitrary point of
is an arbitrary point of  , the analytic continuation of the element
, the analytic continuation of the element  in
in  yields exactly
yields exactly  different elements of the function
different elements of the function  with centre
with centre  ; if
; if  is an arbitrary element with centre
is an arbitrary element with centre  , all the remaining
, all the remaining  elements with centre
elements with centre  can be obtained by analytic continuation along closed paths around the point
can be obtained by analytic continuation along closed paths around the point  ; and 3) the values at the points
; and 3) the values at the points  of
of 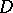 of all elements which are obtainable from
of all elements which are obtainable from  by continuation in
by continuation in  tend to a definite, finite or infinite, limit as
tend to a definite, finite or infinite, limit as  tends to
tends to  while remaining in D.
while remaining in D.
The number  is said to be the order of the algebraic branch point. All branches of the function
is said to be the order of the algebraic branch point. All branches of the function  obtainable by analytic continuation of the element
obtainable by analytic continuation of the element 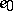 in the annulus
in the annulus 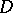 may be represented in a deleted neighbourhood of
may be represented in a deleted neighbourhood of  by a generalized Laurent series (Puiseux series):
by a generalized Laurent series (Puiseux series):
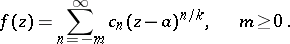 |
The point at infinity,  , is called an algebraic branch point for a function
, is called an algebraic branch point for a function 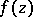 if the point
if the point  is an algebraic branch point of the function
is an algebraic branch point of the function  .
.
There may exist several (and even an infinite number of) different algebraic branch points and regular points of a complete analytic function with a given affix  .
.
References
| [1] | A.I. Markushevich, "Theory of functions of a complex variable" , 3 , Chelsea (1977) pp. Chapt.8 (Translated from Russian) |
| [2] | A. Hurwitz, R. Courant, "Vorlesungen über allgemeine Funktionentheorie und elliptische Funktionen" , 4 , Springer (1968) |
Algebraic branch point. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Algebraic_branch_point&oldid=14573