Algebraic K-theory
A branch of algebra, dealing mainly with the study of the so-called 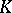 -functors (
-functors (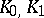 , etc., cf.
, etc., cf. 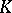 -functor); it is a part of general linear algebra. It deals with the structure theory of projective modules and their automorphism groups. To put it more simply, it is a generalization of results obtained on the existence and uniqueness (up to an automorphism) of a basis of a vector space and other group-theoretical facts concerning linear groups over fields. On passing from a field to an arbitrary ring
-functor); it is a part of general linear algebra. It deals with the structure theory of projective modules and their automorphism groups. To put it more simply, it is a generalization of results obtained on the existence and uniqueness (up to an automorphism) of a basis of a vector space and other group-theoretical facts concerning linear groups over fields. On passing from a field to an arbitrary ring  these theorems usually become invalid, and the Grothendieck group
these theorems usually become invalid, and the Grothendieck group 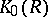 and the Whitehead group
and the Whitehead group 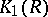 are, in a certain sense, a measure of their deviation from being true. Similar generalizations of the structure theorems of linear algebra appear in topology. A vector space can be regarded as a special case of a vector bundle. These objects may be studied with the aid of the homotopy theory of vector bundles and of topological
are, in a certain sense, a measure of their deviation from being true. Similar generalizations of the structure theorems of linear algebra appear in topology. A vector space can be regarded as a special case of a vector bundle. These objects may be studied with the aid of the homotopy theory of vector bundles and of topological 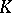 -theory. It is important to note in this connection that a projective module can be regarded as the module of sections of a vector bundle. This explains the choice of the class of projective modules as the object of the theory. Algebraic
-theory. It is important to note in this connection that a projective module can be regarded as the module of sections of a vector bundle. This explains the choice of the class of projective modules as the object of the theory. Algebraic 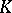 -theory makes extensive use of the theory of rings, homological algebra, category theory and the theory of linear groups.
-theory makes extensive use of the theory of rings, homological algebra, category theory and the theory of linear groups.
Algebraic 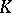 -theory has two different historical origins, both in the field of geometry. The first is related to certain topological obstructions. The starting point was the introduction of the concept of Whitehead torsion, which is connected with the homotopy equivalence of finite complexes and is an element in the Whitehead group, the latter being some quotient group of the group
-theory has two different historical origins, both in the field of geometry. The first is related to certain topological obstructions. The starting point was the introduction of the concept of Whitehead torsion, which is connected with the homotopy equivalence of finite complexes and is an element in the Whitehead group, the latter being some quotient group of the group  , where
, where 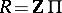 is the integral group ring of the fundamental group
is the integral group ring of the fundamental group 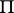 . The next step concerned topological spaces
. The next step concerned topological spaces 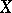 that are dominated by a finite complex, and their generalized Euler characteristic
that are dominated by a finite complex, and their generalized Euler characteristic  , which is an element of group
, which is an element of group 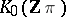 . The computation of the Whitehead group and
. The computation of the Whitehead group and  -groups (which is, strictly speaking, an algebraic problem concerning group rings), was in fact one of the first objectives of algebraic
-groups (which is, strictly speaking, an algebraic problem concerning group rings), was in fact one of the first objectives of algebraic 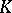 -theory. Both
-theory. Both 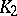 and other higher functors have topological applications of the same type (for example, an obstruction to the deformation of a pseudo-isotopy of a closed manifold into an isotopy lies in some quotient group of the group
and other higher functors have topological applications of the same type (for example, an obstruction to the deformation of a pseudo-isotopy of a closed manifold into an isotopy lies in some quotient group of the group  ). Algebraic studies of the Whitehead group began in the 1940s. A related field is the study of the structure of linear groups over arbitrary rings, in particular, the theory of determinants over a skew-field [10].
). Algebraic studies of the Whitehead group began in the 1940s. A related field is the study of the structure of linear groups over arbitrary rings, in particular, the theory of determinants over a skew-field [10].
The second origin of algebraic 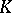 -theory was an algebraic proof of the Riemann–Roch theorem [7] and its generalizations by A. Grothendieck in 1957. These considerations involved the introduction of the
-theory was an algebraic proof of the Riemann–Roch theorem [7] and its generalizations by A. Grothendieck in 1957. These considerations involved the introduction of the  -functor
-functor  as the group of values of a universal additive functor on coherent sheaves on a smooth algebraic variety. Moreover, the previously familiar representation rings, Witt rings (cf. Witt ring) of classes of quadratic forms, etc., turned out to be related constructions. The
as the group of values of a universal additive functor on coherent sheaves on a smooth algebraic variety. Moreover, the previously familiar representation rings, Witt rings (cf. Witt ring) of classes of quadratic forms, etc., turned out to be related constructions. The 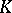 -functor was then transferred to topology, in which it found numerous applications, and with its help several previously unsolved problems could be dealt with.
-functor was then transferred to topology, in which it found numerous applications, and with its help several previously unsolved problems could be dealt with.
It became clear, moreover, that this construction reveals new perspectives in the understanding of old analytical problems (the index problem of elliptic operators), topological problems (extraordinary homology theories), and the theory of group representations. However, the development of algebraic 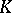 -theory for rings (beginning with the establishment of the correspondence (analogy) between projective, finitely-generated modules and vector bundles) was hindered by the fact that an adequate concept, analogous to that of suspension in topology, was lacking in algebra.
-theory for rings (beginning with the establishment of the correspondence (analogy) between projective, finitely-generated modules and vector bundles) was hindered by the fact that an adequate concept, analogous to that of suspension in topology, was lacking in algebra.
The 1950s and 1960s saw the beginning of the systematic study of projective modules over finite groups, and the development of one of the most important ideas on which algebraic 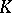 -theory is based — the idea of "stabilization" , the essence of which, roughly speaking, is that general relationships are more clearly manifested on passing to the limit of the dimension of the objects studied (e.g. linear groups or projective modules). Connections were noted between algebraic
-theory is based — the idea of "stabilization" , the essence of which, roughly speaking, is that general relationships are more clearly manifested on passing to the limit of the dimension of the objects studied (e.g. linear groups or projective modules). Connections were noted between algebraic  -theory and the reciprocity laws of the theory of algebraic numbers and algebraic functions; studies were made of problems connected with congruence subgroups (cf. Congruence subgroup) and an algebraic analogue of the Bott periodicity theorem — the theory of polynomial extensions — was obtained.
-theory and the reciprocity laws of the theory of algebraic numbers and algebraic functions; studies were made of problems connected with congruence subgroups (cf. Congruence subgroup) and an algebraic analogue of the Bott periodicity theorem — the theory of polynomial extensions — was obtained.
For a ring  with a unit element, the Grothendieck group
with a unit element, the Grothendieck group 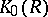 is defined as the Abelian group generated by the isomorphism classes of finitely-generated projective
is defined as the Abelian group generated by the isomorphism classes of finitely-generated projective  -modules, with the defining relation:
-modules, with the defining relation:
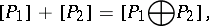 |
where  is the class of modules isomorphic to the module
is the class of modules isomorphic to the module 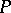 . Let
. Let 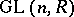 be the general linear group over
be the general linear group over  , let
, let
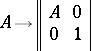 |
be the imbedding of 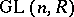 in
in 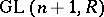 , let
, let 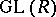 be the direct limit of the groups
be the direct limit of the groups 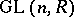 , and let
, and let 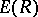 be the subgroup in
be the subgroup in 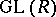 generated by the elementary matrices
generated by the elementary matrices  , i.e. by the matrices that have an element
, i.e. by the matrices that have an element  at the
at the 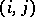 -th place and agree with the unit matrix in all other places.
-th place and agree with the unit matrix in all other places.  then coincides with the commutator of
then coincides with the commutator of  . The quotient group
. The quotient group 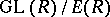 is denoted by
is denoted by 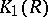 , and is known as the Whitehead group. Finally, the Steinberg group
, and is known as the Whitehead group. Finally, the Steinberg group 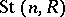 for
for 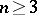 is defined by the generators
is defined by the generators 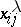 ,
, 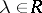 ,
, 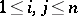 ,
, 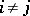 , and the relations
, and the relations
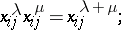 |
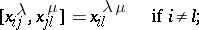 |
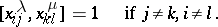 |
Passing to the direct limit, one obtains the group 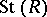 and a natural homomorphism
and a natural homomorphism
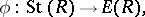 |
with
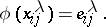 |
The kernel 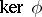 is denoted by
is denoted by  (the Milnor group). It coincides with the centre of
(the Milnor group). It coincides with the centre of 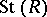 . Thus,
. Thus, 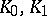 and
and 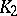 are functors from the category of rings into the category of Abelian groups. Each of the functors
are functors from the category of rings into the category of Abelian groups. Each of the functors  and
and  can be characterized as a functor from finitely-generated projective modules to Abelian groups that satisfies certain properties and is universal with respect to these properties. Such a "universal" characterization makes it possible to define analogues of the functors
can be characterized as a functor from finitely-generated projective modules to Abelian groups that satisfies certain properties and is universal with respect to these properties. Such a "universal" characterization makes it possible to define analogues of the functors  and
and 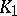 on "sufficiently good" categories. In particular, for the category of Noetherian
on "sufficiently good" categories. In particular, for the category of Noetherian 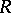 -modules functors
-modules functors 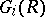 quite close to
quite close to 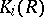 can be defined.
can be defined.
Examples of the groups 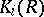 . Let
. Let 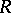 be a skew-field and let
be a skew-field and let 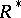 be its multiplicative group.
be its multiplicative group. 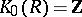 is then the group of integers,
is then the group of integers,  ; and
; and 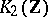 is the cyclic group of order two. If
is the cyclic group of order two. If 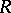 is a finite field, then
is a finite field, then  .
.
An important result in algebraic 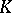 -theory is the exact Mayer–Vietoris sequence for a Cartesian square. The diagram below represents a Cartesian square of ring homomorphisms in which
-theory is the exact Mayer–Vietoris sequence for a Cartesian square. The diagram below represents a Cartesian square of ring homomorphisms in which 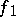 is an epimorphism;
is an epimorphism;
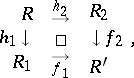 |
then there is an exact sequence
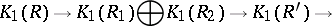 |
 |
If 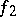 is also an epimorphism, then the sequence is supplemented by the terms
is also an epimorphism, then the sequence is supplemented by the terms
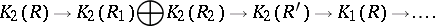 |
If 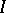 is a two-sided ideal of
is a two-sided ideal of 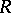 , then the Mayer–Vietoris sequence makes it possible [8] to define the relative functors
, then the Mayer–Vietoris sequence makes it possible [8] to define the relative functors  , which yield an exact sequence
, which yield an exact sequence
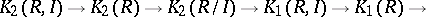 |
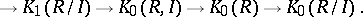 |
A fairly complete study has been made of the behaviour of  -functors on passing from a ring
-functors on passing from a ring  to its localization with respect to a central, multiplicatively-closed system. In particular, if certain conditions on
to its localization with respect to a central, multiplicatively-closed system. In particular, if certain conditions on 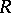 are satisfied, then the following exact sequence has been found for the functor
are satisfied, then the following exact sequence has been found for the functor 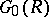 :
:
 |
If 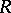 is commutative,
is commutative, 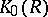 becomes a ring with a unit element by introducing the multiplication induced by the tensor product of modules. There exists a split epimorphism of
becomes a ring with a unit element by introducing the multiplication induced by the tensor product of modules. There exists a split epimorphism of  onto the ring
onto the ring 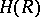 of continuous integer-valued functions (the ring
of continuous integer-valued functions (the ring 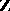 is given the discrete topology) on the spectrum of
is given the discrete topology) on the spectrum of 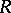 (cf. Spectrum of a ring). The kernel of this homomorphism is denoted by
(cf. Spectrum of a ring). The kernel of this homomorphism is denoted by 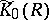 . It is known that
. It is known that 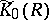 is the nil radical of
is the nil radical of 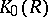 and, if
and, if 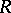 is Noetherian and if the dimension of its maximal spectrum is
is Noetherian and if the dimension of its maximal spectrum is  , then
, then 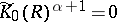 . If this dimension is at most 1, then
. If this dimension is at most 1, then 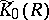 is isomorphic to the Picard group
is isomorphic to the Picard group 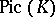 .
.
For arithmetical rings there are finiteness theorems for the functors 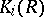 and
and 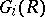 . In fact, if
. In fact, if 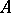 is the ring of integers or the ring of polynomials over a finite field, and
is the ring of integers or the ring of polynomials over a finite field, and 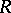 is an
is an 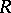 -order and at the same time an
-order and at the same time an 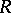 -lattice in a semi-simple finite-dimensional algebra over the field of fractions of a ring
-lattice in a semi-simple finite-dimensional algebra over the field of fractions of a ring 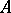 , then the groups
, then the groups 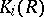 and
and 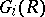 are finitely generated (
are finitely generated (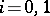 ).
).
The development of algebraic 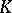 -theory was stimulated by studies carried out on the problem of congruence subgroups: Do all subgroups of finite index in an arithmetical group contain some congruence subgroup? This question is closely connected with the problem of computing the group
-theory was stimulated by studies carried out on the problem of congruence subgroups: Do all subgroups of finite index in an arithmetical group contain some congruence subgroup? This question is closely connected with the problem of computing the group 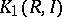 for ideals
for ideals 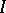 in
in 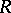 .
.
Of the results concerning the stable structure of projective modules one can mention the following theorem: If 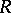 is a commutative Noetherian ring whose maximal spectrum has dimension
is a commutative Noetherian ring whose maximal spectrum has dimension 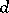 , and
, and 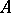 is a module-finite
is a module-finite 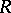 -algebra, then any finitely-generated projective
-algebra, then any finitely-generated projective 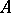 -module
-module 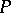 such that
such that
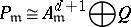 |
for all maximal ideals 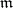 of
of 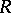 is isomorphic to
is isomorphic to 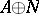 (here
(here 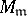 is the localization of the module
is the localization of the module 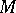 at
at 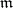 ). Another important theorem on the structure of projective modules is the cancellation theorem: Let
). Another important theorem on the structure of projective modules is the cancellation theorem: Let 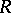 ,
, 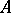 and the module
and the module 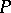 be as above. Let
be as above. Let  be a finitely-generated projective
be a finitely-generated projective 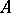 -module, and let
-module, and let 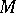 and
and 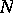 be arbitrary
be arbitrary 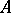 -modules. Then it follows from
-modules. Then it follows from 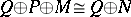 that
that
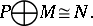 |
The stable rank of a ring 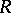 is closely connected with problems of the stable structure of projective modules. Thus, if
is closely connected with problems of the stable structure of projective modules. Thus, if  is a commutative ring of stable rank smaller than
is a commutative ring of stable rank smaller than 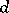 , then
, then
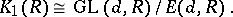 |
In connection with the theory of induced representations of groups, the functors 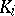 for group rings have been studied. One of the results of these studies is that if
for group rings have been studied. One of the results of these studies is that if 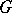 is a finite group of order
is a finite group of order  and
and 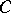 is the set of cyclic subgroups of
is the set of cyclic subgroups of 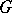 , then the index of the subgroup
, then the index of the subgroup
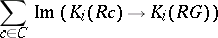 |
in 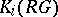 is divisible by
is divisible by  if
if 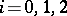 .
.
Regarding polynomial ring extensions it is known that if 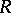 is a regular ring, then
is a regular ring, then
 |
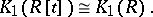 |
Moreover, the sequence
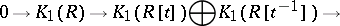 |
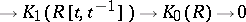 |
is exact for any ring 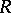 .
.
One result in the computation of the functor 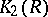 is the theorem of Matsumoto: If
is the theorem of Matsumoto: If  is a field, then
is a field, then 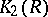 is given by the generators
is given by the generators 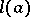 (which are in one-to-one correspondence with all the non-zero elements
(which are in one-to-one correspondence with all the non-zero elements  of
of 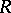 ) and the relations
) and the relations 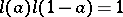 for
for 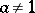 .
.
In the 1970s there appeared numerous versions of the definitions of the functors  for
for 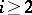 . It has been shown [9] that these theories coincide and yield the classical functors
. It has been shown [9] that these theories coincide and yield the classical functors 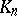 if
if 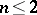 . In several cases effective methods of computation for higher
. In several cases effective methods of computation for higher  -groups were found. The development of unitary
-groups were found. The development of unitary 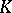 -theory ([9], Vol. 3), which studies analogous problems for modules on which quadratic and bilinear forms are defined, also began in that decade.
-theory ([9], Vol. 3), which studies analogous problems for modules on which quadratic and bilinear forms are defined, also began in that decade.
References
| [1] | M.F. Atiyah, " -theory: lectures" , Benjamin (1967) -theory: lectures" , Benjamin (1967) |
| [2] | H. Bass, "Lectures on topics in algebraic 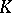 -theory" , Tata Inst. (1966) -theory" , Tata Inst. (1966) |
| [3] | H. Bass, "Algebraic 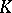 -theory" , Benjamin (1968) -theory" , Benjamin (1968) |
| [4] | R.G. Swan, "Algebraic 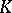 -theory" , Springer (1968) -theory" , Springer (1968) |
| [5] | R.G. Swan, E.G. Evans, " -theory of finite groups and orders" , Springer (1970) -theory of finite groups and orders" , Springer (1970) |
| [6] | C.B. Thomas (ed.) R.M.F. Moss (ed.) , Algebraic  -theory and its geometric applications , Springer (1969) -theory and its geometric applications , Springer (1969) |
| [7] | Yu.I. Manin, "Lectures on the 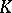 -functor in algebraic geometry" Russian Math. Surveys , 24 : 5 (1969) pp. 1–89 Uspekhi Mat. Nauk , 24 : 5 (1969) pp. 3–86 -functor in algebraic geometry" Russian Math. Surveys , 24 : 5 (1969) pp. 1–89 Uspekhi Mat. Nauk , 24 : 5 (1969) pp. 3–86 |
| [8] | J.W. Milnor, "Introduction to algebraic 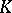 -theory" , Princeton Univ. Press (1971) -theory" , Princeton Univ. Press (1971) |
| [9] | H. Bass (ed.) , Algebraic 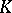 -theory (Battelle Inst. Conf.) , 1–3 , Springer (1973) -theory (Battelle Inst. Conf.) , 1–3 , Springer (1973) |
| [10] | E. Artin, "Geometric algebra" , Interscience (1957) |
Comments
Algebraic 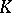 -theoretic ideas and results have become most important in certain parts of functional analysis centering around
-theoretic ideas and results have become most important in certain parts of functional analysis centering around 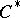 -algebras (cf.
-algebras (cf. 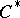 -algebra). Especially in the form of
-algebra). Especially in the form of  -theory (or Kasparov
-theory (or Kasparov 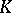 -theory). Cf. e.g. [a2].
-theory). Cf. e.g. [a2].
In algebraic geometry there are important connections with the Chow groups (cf. Chow ring).
References
| [a1] | B. Magurn (ed.) , Reviews in 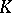 -theory 1940–1984 , Amer. Math. Soc. (1985) -theory 1940–1984 , Amer. Math. Soc. (1985) |
| [a2] | J. Curtz, "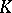 -theory and -theory and 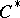 -algebras" A. Bak (ed.) , Algebraic -algebras" A. Bak (ed.) , Algebraic 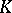 -theory, number theory and analysis , Springer (1984) pp. 55–79 -theory, number theory and analysis , Springer (1984) pp. 55–79 |
Algebraic K-theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Algebraic_K-theory&oldid=15642