Algebra of sets
A non-empty collection of subsets of some set  that is closed under the set-theoretic operations (of union, intersection, taking complements), carried out a finite number of times. In order for a class of subsets of a set
that is closed under the set-theoretic operations (of union, intersection, taking complements), carried out a finite number of times. In order for a class of subsets of a set  to be an algebra of sets, it is necessary (and sufficient) for it to be closed under finite unions and taking the complement. An algebra of sets that is closed under countable unions is known as a
to be an algebra of sets, it is necessary (and sufficient) for it to be closed under finite unions and taking the complement. An algebra of sets that is closed under countable unions is known as a 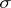 -algebra of sets. Any
-algebra of sets. Any 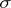 -algebra of sets is closed under the set-theoretic operations carried out a countable number of times.
-algebra of sets is closed under the set-theoretic operations carried out a countable number of times.
Examples.
1) The collection of finite subsets of an arbitrary set  and their complements is an algebra of sets; the collection consisting of the at most countable subsets of
and their complements is an algebra of sets; the collection consisting of the at most countable subsets of  and their complements is a
and their complements is a 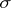 -algebra of sets.
-algebra of sets.
2) The collection of finite unions of intervals of the type
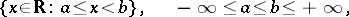 |
forms an algebra of sets.
3) let  be a topological space; the
be a topological space; the 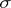 -algebra
-algebra 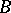 of sets generated by the open subsets of
of sets generated by the open subsets of  (in other words, the smallest
(in other words, the smallest 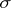 -algebra of sets containing all open subsets of
-algebra of sets containing all open subsets of  ) is known as the Borel
) is known as the Borel 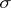 -algebra of subsets of
-algebra of subsets of  , while the sets belonging to
, while the sets belonging to 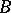 are known as Borel sets.
are known as Borel sets.
4) let 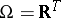 , where
, where  is an arbitrary set (i.e.
is an arbitrary set (i.e.  is the set of all real functions on
is the set of all real functions on 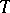 ); the class
); the class 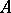 of sets of the type
of sets of the type
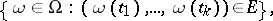 |
where 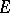 is a Borel subset of
is a Borel subset of 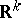 , is an algebra of sets; in the theory of random processes a probability measure is often originally defined only on an algebra of this type, and is their subsequently extended to a wider class of sets (to the
, is an algebra of sets; in the theory of random processes a probability measure is often originally defined only on an algebra of this type, and is their subsequently extended to a wider class of sets (to the 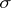 -algebra generated by
-algebra generated by 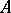 ).
).
5) The collection of Lebesgue-measurable subsets of 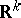 is a
is a 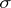 -algebra of sets.
-algebra of sets.
Algebras (respectively, 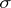 -algebras) are the natural domain of definition of finitely-additive (respectively,
-algebras) are the natural domain of definition of finitely-additive (respectively, 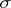 -additive) measures. According to the theorem of extension of measures, any
-additive) measures. According to the theorem of extension of measures, any 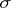 -finite,
-finite, 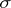 -additive measure, defined on an algebra
-additive measure, defined on an algebra 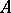 , can be uniquely extended to a
, can be uniquely extended to a 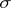 -additive measure defined on the
-additive measure defined on the 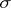 -algebra generated by
-algebra generated by 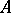 .
.
References
| [1] | N. Dunford, J.T. Schwartz, "Linear operators. General theory" , 1 , Interscience (1958) |
| [2] | P.R. Halmos, "Measure theory" , v. Nostrand (1950) |
| [3] | J. Neveu, "Bases mathématiques du calcul des probabilités" , Masson (1970) |
Algebra of sets. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Algebra_of_sets&oldid=15704