Aleksandrov problem for isometric mappings
Let 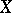 ,
, 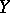 be two metric spaces, with respective distances
be two metric spaces, with respective distances 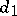 ,
, 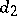 (cf. also Metric space). A mapping
(cf. also Metric space). A mapping 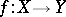 is defined to be an isometry if
is defined to be an isometry if 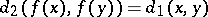 for all
for all 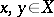 . A mapping
. A mapping  is said to preserve the distance
is said to preserve the distance  if for all
if for all 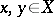 with
with 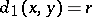 one has
one has 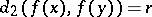 . A.D. Aleksandrov has posed the problem whether the existence of a single preserved distance for some mapping
. A.D. Aleksandrov has posed the problem whether the existence of a single preserved distance for some mapping 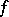 implies that
implies that 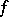 is an isometry (cf. [a1]).
is an isometry (cf. [a1]).
Even if  ,
, 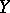 are normed vector spaces, the above problem is not easy to answer (note that, in this case, taking
are normed vector spaces, the above problem is not easy to answer (note that, in this case, taking 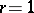 is no loss of generality). For example, the following question has not been solved yet (as of 2000): Is a mapping
is no loss of generality). For example, the following question has not been solved yet (as of 2000): Is a mapping 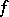 from
from 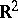 to
to 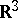 preserving unit distance necessarily an isometry (cf. [a17])?
preserving unit distance necessarily an isometry (cf. [a17])?
The discussion of Aleksandrov's problem under certain additional conditions on the given mapping preserving unit distance has led to several interesting and new problems (cf. [a14], [a15], [a16], [a18], [a17]).
The Aleksandrov problem has been solved for Euclidean spaces 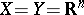 : For
: For 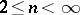 , the answer is positive [a2], while for
, the answer is positive [a2], while for 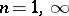 , the answer is negative [a2], [a5], [a13]. In general normed vector spaces, the answer is positive for a mapping that is contractive, surjective and preserves the unit distance. The problem also has a positive solution when
, the answer is negative [a2], [a5], [a13]. In general normed vector spaces, the answer is positive for a mapping that is contractive, surjective and preserves the unit distance. The problem also has a positive solution when 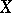 and
and 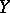 are strictly convex vector spaces, provided
are strictly convex vector spaces, provided 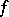 is a homeomorphism and the dimension of
is a homeomorphism and the dimension of 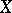 is greater than
is greater than  (cf. [a12], [a20]).
(cf. [a12], [a20]).
The Aleksandrov problem has also been solved in some special cases of mappings 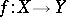 which preserve two distances with an integer ratio greater than
which preserve two distances with an integer ratio greater than 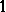 , with
, with 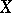 and
and 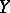 strictly convex vector spaces and the dimension of
strictly convex vector spaces and the dimension of 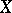 greater than
greater than  (cf. [a3], [a16], [a17]). Furthermore, when
(cf. [a3], [a16], [a17]). Furthermore, when 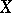 ,
, 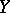 are Hilbert spaces and the dimension of
are Hilbert spaces and the dimension of 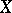 is greater than
is greater than  , a lot of work has been done (cf. [a21], [a22], [a23]; for example, when
, a lot of work has been done (cf. [a21], [a22], [a23]; for example, when 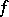 preserves the two distances
preserves the two distances 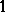 and
and 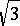 ; when
; when 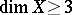 and
and 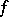 preserves
preserves 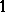 and
and 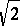 , then
, then 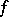 is an affine isometry, etc.).
is an affine isometry, etc.).
Problems connected with stability of isometries as well as non-linear perturbations of isometries have been extensively studied in [a4], [a5], [a6], [a7], [a8], [a9], [a10], [a11].
References
| [a1] | A.D. Aleksandrov, "Mapping of families of sets" Soviet Math. Dokl. , 11 (1970) pp. 116–120 |
| [a2] | F.S. Beckman, D.A. Quarles, "On isometries of Euclidean spaces" Proc. Amer. Math. Soc. , 4 (1953) pp. 810–815 |
| [a3] | W. Benz, H. Berens, "A contribution to a theorem of Ulam–Mazur" Aquat. Math. , 34 (1987) pp. 61–63 |
| [a4] | D.G. Bourgain, "Approximate isometries" Bull. Amer. Math. Soc. , 52 (1946) pp. 704–714 |
| [a5] | K. Ciesielski, Th.M. Rassias, "On some properties of isometric mappings" Facta Univ. Ser. Math. Inform. , 7 (1992) pp. 107–115 |
| [a6] | G. Dolinar, "Generalized stability of isometries" J. Math. Anal. Appl. , 202 (2000) pp. 39–56 |
| [a7] | J. Gevirtz, "Stability of isometries on Banach spaces" Proc. Amer. Math. Soc. , 89 (1983) pp. 633–636 |
| [a8] | P.M. Gruber, "Stability of isometries" Trans. Amer. Math. Soc. , 245 (1978) pp. 263–277 |
| [a9] | J. Lindenstrauss, A. Szankowski, "Non linear perturbations of isometries" Astérisque , 131 (1985) pp. 357–371 |
| [a10] | D.H. Hyers, S.M. Mazur, "On approximate isometries" Bull. Amer. Math. Soc. , 51 (1945) pp. 288–292 |
| [a11] | S.M. Mastir, S. Ulam, "Sur les transformations isométriques d'espaces vectoriels normés" C.R. Acad. Sci. Paris , 194 (1932) pp. 946–948 |
| [a12] | B. Mielnik, Th.M. Rassias, "On the Aleksandrov problem of conservative distances" Proc. Amer. Math. Soc. , 116 (1992) pp. 1115–1118 |
| [a13] | Th.M. Rassias, "Some remarks on isometric mappings" Facta Univ. Ser. Math. Inform. , 2 (1987) pp. 49–52 |
| [a14] | Th.M. Rassias, "Is a distance one preserving maping between metric space always an isometry?" Amer. Math. Monthly , 90 (1983) pp. 200 |
| [a15] | Th.M. Rassias, "The stability of linear mappings and some problems on isometries" , Proc. Internat. Conf. Math. Anal. Appl. Kuwait, 1985 , Pergamon (1988) pp. 175–184 |
| [a16] | Th.M. Rassias, "Mappings that preserve unit distance" Indian J. Math. , 32 (1990) pp. 275–278 |
| [a17] | Th.M. Rassias, "Properties of isometries and approximate isometries" , Recent Progress in Inequalities , Kluwer Acad. Publ. (1998) pp. 325–345 |
| [a18] | Th.M. Rassias, "Remarks and problems" Aequat. Math. , 39 (1990) pp. 304 |
| [a19] | Th.M. Rassias, "Remarks and problems" Aequat. Math. , 56 (1998) pp. 304–306 |
| [a20] | Th.M. Rassias, P. Semrl, "On the Masur–Ulam theorem and the Aleksandrov probiem for unit distance preserving mapping" Proc. Amer. Math. Soc. , 118 (1993) pp. 919–925 |
| [a21] | Th.M. Rassias, Shuhuang Xiang, "On mappings with conservative distance and the Mazur–Ulam theorem" Publ. EPT. , to appear (2000) |
| [a22] | Shuhuang Xiang, "Aleksandrov problem and mappings which preserves distances" , Funct. Equations and Inequalities , Kluwer Acad. Publ. (2000) pp. 297–323 |
| [a23] | Shuhuang Xiang, "Mappings of conservative distances and the Mazur–Ulam theorem" J. Math. Anal. Appl. , 254 (2001) pp. 262–274 |
Aleksandrov problem for isometric mappings. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Aleksandrov_problem_for_isometric_mappings&oldid=17029