Difference between revisions of "Aleksandrov-Čech homology and cohomology"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (moved Aleksandrov–Čech homology and cohomology to Aleksandrov-Cech homology and cohomology: ascii title) |
Revision as of 17:36, 24 March 2012
spectral homology and cohomology
Homology and cohomology theories which satisfy all Steenrod–Eilenberg axioms (except, possibly, the exactness axiom) and a certain continuity condition. The Aleksandrov–Čech homology groups (modules) 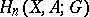 [1], [2] are defined as the inverse limit
[1], [2] are defined as the inverse limit  over all open coverings
over all open coverings  of the space
of the space  ; here
; here  signifies not only the covering, but also its nerve, and
signifies not only the covering, but also its nerve, and  is the subcomplex in
is the subcomplex in  that is the nerve of the restriction of
that is the nerve of the restriction of  on the closed set
on the closed set  (cf. Nerve of a family of sets). The possibility of passing to the limit is ensured by the existence of simplicial projections
(cf. Nerve of a family of sets). The possibility of passing to the limit is ensured by the existence of simplicial projections  defined, up to an homotopy, by the inclusion of
defined, up to an homotopy, by the inclusion of  in
in  . The Aleksandrov–Čech cohomology groups
. The Aleksandrov–Čech cohomology groups  are defined as the direct limit
are defined as the direct limit 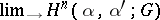 . The homology groups satisfy all the Steenrod–Eilenberg axioms except for the exactness axiom. All axioms are valid for cohomology, and, partly for this reason, cohomology is often more useful. The exactness axiom is also valid for homology on the category of compacta if
. The homology groups satisfy all the Steenrod–Eilenberg axioms except for the exactness axiom. All axioms are valid for cohomology, and, partly for this reason, cohomology is often more useful. The exactness axiom is also valid for homology on the category of compacta if  is a compact group or field. In addition, Aleksandrov–Čech homology and cohomology groups have the property of continuity: For
is a compact group or field. In addition, Aleksandrov–Čech homology and cohomology groups have the property of continuity: For  the homology (cohomology) groups in addition are equal to the respective limit of the homology (cohomology) groups of the compacta
the homology (cohomology) groups in addition are equal to the respective limit of the homology (cohomology) groups of the compacta  . The Aleksandrov–Čech theory is the only theory satisfying the Steenrod–Eilenberg axioms (with the exception indicated above) and this condition of continuity. On the category of paracompact spaces, the usual characterization by mappings into Eilenberg–MacLane spaces is valid for cohomology; while the cohomology itself is equivalent to the cohomology defined in sheaf theory. Cohomology may also be defined as cohomology of some cochain complex, which makes it possible to operate with sheaves of cochains. Similar ideas, applied to homology, are contained in the homology theory originating from N. Steenrod, A. Borel and others, which satisfies all axioms including the exactness axiom (but the property of continuity is lost). Aleksandrov–Čech homology and cohomology, including the above modification, are employed in homological problems in the theory of continuous mappings, in the theory of transformation groups (a connection with quotient spaces), in the theory of generalized manifolds (in particular, in various duality relations), in the theory of analytic spaces (e.g. in defining the fundamental classes of homology), in homological dimension theory, etc.
. The Aleksandrov–Čech theory is the only theory satisfying the Steenrod–Eilenberg axioms (with the exception indicated above) and this condition of continuity. On the category of paracompact spaces, the usual characterization by mappings into Eilenberg–MacLane spaces is valid for cohomology; while the cohomology itself is equivalent to the cohomology defined in sheaf theory. Cohomology may also be defined as cohomology of some cochain complex, which makes it possible to operate with sheaves of cochains. Similar ideas, applied to homology, are contained in the homology theory originating from N. Steenrod, A. Borel and others, which satisfies all axioms including the exactness axiom (but the property of continuity is lost). Aleksandrov–Čech homology and cohomology, including the above modification, are employed in homological problems in the theory of continuous mappings, in the theory of transformation groups (a connection with quotient spaces), in the theory of generalized manifolds (in particular, in various duality relations), in the theory of analytic spaces (e.g. in defining the fundamental classes of homology), in homological dimension theory, etc.
References
| [1] | P.S. [P.S. Aleksandrov] Aleksandroff, "Untersuchungen über Gestalt und Lage abgeschlossener Mengen beliebiger Dimension" Ann. of Math. (2) , 30 (1929) pp. 101–187 |
| [2] | E. Čech, "Théorie générale de l'homologie dans un espace quelconque" Fund. Math. , 19 (1932) pp. 149–183 |
| [3] | N.E. Steenrod, S. Eilenberg, "Foundations of algebraic topology" , Princeton Univ. Press (1966) |
| [4] | E.G. Sklyarenko, "Homology theory and the exactness axiom" Russian Math. Surveys , 24 : 5 (1969) pp. 91–142 Uspekhi Mat. Nauk , 24 : 5 (1969) pp. 87–140 |
Comments
Often one speaks also of Čech cohomology instead of Aleksandrov–Čech cohomology.
Aleksandrov-Čech homology and cohomology. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Aleksandrov-%C4%8Cech_homology_and_cohomology&oldid=16910