Airy equation
The second-order linear ordinary differential equation
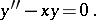 |
It occurred first in G.B. Airy's research in optics [1]. Its general solution can be expressed in terms of Bessel functions of order  :
:
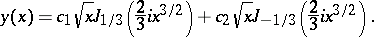 |
Since the Airy equation plays an important role in various problems of physics, mechanics and asymptotic analysis, its solutions are regarded as forming a distinct class of special functions (see Airy functions).
The solutions of the Airy equation in the complex plane  ,
,
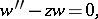 |
have the following fundamental properties:
1) Every solution is an entire function of  and can be expanded in a power series
and can be expanded in a power series
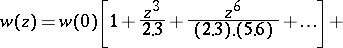 |
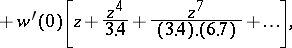 |
which converges for all  .
.
2) If 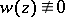 is a solution of the Airy equation, then so are
is a solution of the Airy equation, then so are 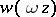 and
and 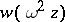 , where
, where 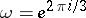 , and any two of these solutions are linearly independent. The following identity holds:
, and any two of these solutions are linearly independent. The following identity holds:
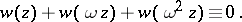 |
References
| [1] | G.B. Airy, "On the intensity of light in the neighbourhood of a caustic" Trans. Cambridge Philos. Soc. , 6 (1838) pp. 379–402 |
| [2] | V.M. Babich, V.S. Buldyrev, "Asymptotic methods in the diffraction of short waves" , Moscow (1972) (In Russian) (Translation forthcoming: Springer) |
| [3] | M. Abramowitz (ed.) I.A. Stegun (ed.) , Handbook of mathematical functions , Appl. Math. Series , 55 , Nat. Bureau of Standards,, U.S. Department Commerce (1964) |
Airy equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Airy_equation&oldid=15069