Age-structured population
The mathematical modeling of age-structured populations has been initiated by the pioneering work of A.J. Lotka and A.C. McKendrick in the years 1920–1940 (see [a6], [a7], [a8]). For a long time, the interest in age-structure was restricted mainly to demography, but in recent years a new impulse to the research came from other fields and nowadays (1990s) age-structure plays a fundamental role in ecology, epidemiology, cell growth, etc.. As a matter of fact, age is one of the most natural and important parameters structuring a population, because many internal variables, at the level of the single individual, are strictly depending on the age, so that differing ages imply different reproduction and survival capacities and, also, different behaviours.
The basic linear model, usually named the Lotka–McKendrick model, describes the growth of a single population under the assumption that age is the only source of difference among individuals. It is the equivalent of Malthusian growth for a homogeneous population. The state of the population is described by its age-distribution $p ( a , t )$, where $a$ and $t$ denote age and time, respectively; namely
\begin{equation*} \int _ { a _ { 1 } } ^ { a _ { 2 } } p ( a , t ) d a \end{equation*}
is the number of individuals of the population that at time $t$ have ages in the interval $[ a _ { 1 } , a _ { 2 } ]$. The dynamics is based on the following Cauchy problem
\begin{equation} \tag{a1} \left\{ \begin{array} { l } { p_{ t } ( a , t ) + p _ { a } ( a , t ) + \mu ( a ) p ( a , t ) = 0, } \\ { p ( 0 , t ) = \int _ { 0 } ^ { + \infty } \beta ( a ) p ( a , t ) d a, } \\ { p ( a , 0 ) = p _ { 0 } ( a ) \geq 0, } \end{array} \right. \end{equation}
where $\beta ( a )$ and $\mu ( a )$ are the age-specific fertility and mortality rate, respectively. Thus,
\begin{equation*} b ( t ) = \int _ { 0 } ^ { + \infty } \beta ( a ) p ( a , t ) d a \end{equation*}
is the (total) birth rate at time $t$ and
\begin{equation*} \Pi ( a ) = \operatorname { exp } \left( - \int _ { 0 } ^ { a } \mu ( \sigma ) d \sigma \right) \end{equation*}
is the survival probability, i.e. the probability that an individual will survive until age $a$.
In problem (a1), the first equation describes the aging process, while the boundary condition (the second equation) gives the renewal of the population through the input of newborns. This latter condition is a non-local one and makes the problem related to integral equations of Volterra type (cf. also Volterra equation). In fact, the solution of (a1) has the form
\begin{equation} \tag{a2} p ( a , t ) = \left\{ \begin{array} { l l } { p _ { 0 } ( a - t ) \frac { \Pi ( a ) } { \Pi ( a - t ) } } & { \text { if } a \geq t, } \\ { b ( t - a ) \Pi ( a ) } & { \text { if } a < t, } \end{array} \right. \end{equation}
where the birth rate $b ( t )$ is the solution of the Volterra equation of the first kind
\begin{equation} \tag{a3} b ( t ) = F ( t ) + \int _ { 0 } ^ { t } K ( t - s ) b ( s ) d s \end{equation}
and
\begin{equation} \tag{a4} F ( t ) = \int _ { t } ^ { + \infty } p _ { 0 } ( a - t ) \frac { \Pi ( a ) } { \Pi ( a - t ) } d a, \end{equation}
\begin{equation*} K ( t ) = \beta ( t ) \Pi ( t ). \end{equation*}
A fundamental result concerning the asymptotic behaviour of $p ( a , t )$ states that
\begin{equation} \tag{a5} p ( a , t ) = \operatorname c_0 e ^ { \lambda ^ { * } ( t - a ) } \Pi ( a ) ( 1 + \Omega ( t - a ) ), \end{equation}
where $c_0 \geq 0$ and $\operatorname { lim } _ { t \rightarrow + \infty } \Omega ( t ) = 0$. Here, $\lambda ^ { * }$ is the only real root of the so-called Lotka characteristic equation
\begin{equation} \tag{a6} \int _ { 0 } ^ { + \infty } e ^ { - \lambda a } \beta ( a ) \Pi ( a ) d a = 1, \end{equation}
any other root being non-real and with real part strictly less than $\lambda ^ { * }$. The particular solution $p ^ { * } ( a , t ) = c_{0} e ^ { \lambda ^ { * } ( t - a ) } \Pi ( a ) = e ^ { \lambda ^ { * } t } w ^ { * } ( a ) $, which is the asymptotic limit of $p ( a , t )$ in the sense stated by (a5), is called a persistent solution and corresponds to a stable age-profile $w ^ { * } ( a )$. The basic parameter $\lambda ^ { * }$ is called the intrinsic Malthusian parameter and is strictly related to the so-called net reproduction rate
\begin{equation*} R = \int _ { 0 } ^ { + \infty } \beta ( a ) \Pi ( a ) d a, \end{equation*}
which represents the number of newborns that a single individuals produces in his lifetime; thus, $\lambda ^ { * } > 0$ (respectively, $< 0$ or $= 0$) when $R > 1$ (respectively, $< 1$ or $= 1$). The asymptotic behaviour stated in (a5) is also referred to as the ergodic property, according to which the population forgets its initial age distribution, eventually attaining the stable profile $w ^ { * } ( a )$.
Non-linear models, taking into account logistic effects and other mechanisms of the inter-specific interaction may be conceived in a large variety of ways describing how the age distribution influences the vital rates. A fairly general and often-used model is the following version of a model first proposed by M.E. Gurtin and R.C. MacCamy in [a3]
\begin{equation} \tag{a7} \begin{cases} { p _ { t } ( a , t ) + p _ { a } ( a , t ) + \mu ( a , S ( t ) ) p ( a , t ) = 0 }, \\ { p ( 0 , t ) = \int ^ { + \infty_0 } \beta ( \sigma , s ( t ) ) p ( \sigma , t ) d \sigma }, \\ { p ( a , 0 ) = p_ 0(a) }, \\ { S ( t ) = \int^{+\infty_0} \gamma ( \sigma ) p ( \sigma , t ) d \sigma . } \end{cases}. \end{equation}
Here, fertility and mortality depend upon the population through a variable $S ( t )$ which is a weighted selection of the distribution. Stationary states for problem (a7) have the form
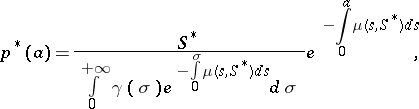 | (a8) |
where $S ^ { * }$ is a solution of the equation
\begin{equation} \tag{a9} \int _ { 0 } ^ { + \infty } \beta ( \sigma , S ^ { * } ) e ^ { - \int _ { 0 } ^ { \sigma } \mu ( s , S ^ { * } ) d s } d \sigma = 1. \end{equation}
This equation means that at the equilibrium size $S ^ { * }$ the net reproduction rate of the population must be equal to $1$. The stability analysis of stationary states involves the investigation of a transcendental characteristic equation. Depending upon its own structure, the model may show different behaviour, including existence of stable periodic solutions.
Significant specific examples of (a7) are the birth-logistic model
\begin{equation*} \mu ( a , x ) = \mu _ { 0 } ( a ), \end{equation*}
\begin{equation*} \beta ( a , x ) = R \beta _ { 0 } ( a ) \Phi ( x ) \end{equation*}
where $\Phi ( x )$ is a decreasing function, and the cannibalism model
\begin{equation*} \mu ( a , x ) = \mu _ { 0 } ( a ) + \mu _ { 1 } ( a ) K \Psi ( x ), \end{equation*}
\begin{equation*} \beta ( a , x ) = \beta _ { 0 } ( a ) \end{equation*}
where $\Psi ( x )$ is increasing.
Beyond single species models, age structure is considered in many multi-population systems. In the domain of demography, two-sex models are of special interest and in the context of ecology the different cases of the inter-specific interaction are studied.
A well-investigated field is epidemics modeling, where age structure is taken into account for the description of diseases whose transmission strongly depends on particular age classes; typical examples are, of course, childhood diseases, as opposed to sexual transmitted ones. The analysis of the models shows that age structure may be responsible for periodicity in the outbreak of the disease.
In the same context of epidemics, a different kind of age structure is also considered; in fact, the so-called class age, i.e. the time elapsed since an individual has become infected, plays a role when variable infectiveness has to be considered. The description of the HIV/AIDS epidemic, with its long incubation period, requires that both chronological age and class age be taken into account.
The mathematical methods involved in the study of age-structured populations include: direct methods, which are widely used, and specific techniques from the theory of Volterra integral and integro-differential equations; however, in recent years, a functional-analytic approach based on the theory of semi-groups of operators (cf. also Semi-group of operators) has also provided a natural and powerful framework for the research in this field (see [a2]).
References
| [a1] | A.J. Coale, "The growth and structure of human populations. A mathematical investigation" , Princeton Univ. Press (1972) |
| [a2] | G. Webb, "Theory of nonlinear age-dependent population dynamics" , M. Dekker (1985) |
| [a3] | M.E. Gurtin, R.C. MacCamy, "Nonlinear age-dependent population dynamics" Arch. Rat. Mech. Anal. , 54 (1974) pp. 281–300 |
| [a4] | J. Impagliazzo, "Deterministic aspects of mathematical demography" , Biomathematics , 13 , Springer (1985) |
| [a5] | N. Keyfitz, "Introduction to the mathematics of populations with revisions" , Addison-Wesley (1977) |
| [a6] | A.J. Lotka, "On a integral equation in population analysis" Ann. Math. Stat. , 10 (1939) pp. 1–25 |
| [a7] | A.J. Lotka, "The stability of the normal age distribution" Proc. Nat. Acad. Sci. , 8 (1922) pp. 339–345 |
| [a8] | A.C. McKendrick, "Applications of mathematics to medical problems" Proc. Edinburgh Math. Soc. , 44 (1926) pp. 98–130 |
| [a9] | J.A.J. Metz, O. Diekmann, "The Dynamics of physiologically structured populations" , Lecture Notes Biomath. , 68 , Springer (1986) |
| [a10] | J. Song, J. Yu, "Population system control" , Springer (1980) |
Age-structured population. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Age-structured_population&oldid=50785