Affine morphism
A morphism of schemes 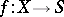 such that the pre-image of any open affine subscheme in
such that the pre-image of any open affine subscheme in  is an affine scheme. The scheme
is an affine scheme. The scheme 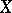 is called an affine
is called an affine  -scheme.
-scheme.
Let 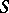 be a scheme, let
be a scheme, let 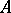 be a quasi-coherent sheaf of
be a quasi-coherent sheaf of 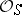 -algebras and let
-algebras and let  be open affine subschemes in
be open affine subschemes in 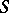 which form a covering of
which form a covering of 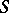 . Then the glueing of the affine schemes
. Then the glueing of the affine schemes 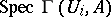 determines an affine
determines an affine 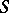 -scheme, denoted by
-scheme, denoted by 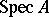 . Conversely, any affine
. Conversely, any affine 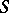 -scheme definable by an affine morphism
-scheme definable by an affine morphism 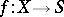 is isomorphic (as a scheme over
is isomorphic (as a scheme over 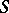 ) to the scheme
) to the scheme 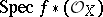 . The set of
. The set of 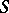 -morphisms of an
-morphisms of an 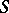 -scheme
-scheme 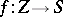 into the affine
into the affine 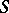 -scheme
-scheme 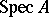 is in bijective correspondence with the homomorphisms of the sheaves of
is in bijective correspondence with the homomorphisms of the sheaves of 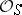 -algebras
-algebras 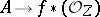 .
.
Closed imbeddings of schemes or arbitrary morphisms of affine schemes are affine morphisms; other examples of affine morphisms are entire morphisms and finite morphisms. Thus the morphism of normalization of a scheme is an affine morphism. Under composition and base change the property of a morphism to be an affine morphism is preserved.
References
| [1] | A. Grothendieck, "The cohomology theory of abstract algebraic varieties" , Proc. Internat. Math. Congress Edinburgh, 1958 , Cambridge Univ. Press (1960) pp. 103–118 |
| [2] | J. Dieudonné, A. Grothendieck, "Elements de géometrie algébrique" Publ. Math. IHES , 4 (1960) |
Comments
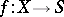 is a finite morphism if there exist a covering
is a finite morphism if there exist a covering 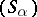 of
of 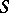 by affine open subschemes such that
by affine open subschemes such that 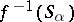 is affine for all
is affine for all  and such that the ring
and such that the ring 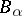 of
of  is finitely generated as a module over the ring
is finitely generated as a module over the ring 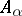 of
of  . The morphism is entire if
. The morphism is entire if 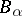 is entire over
is entire over 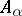 , i.e. if every
, i.e. if every 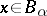 integral over
integral over 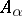 , which means that it is a root of a monic polynomial with coefficients in
, which means that it is a root of a monic polynomial with coefficients in 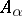 , or, equivalently, if for each
, or, equivalently, if for each 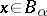 the module
the module 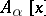 is a finitely-generated module over
is a finitely-generated module over 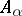 .
.
References
| [a1] | R. Hartshorne, "Algebraic geometry" , Springer (1977) |
Affine morphism. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Affine_morphism&oldid=19150