Affine algebraic set
affine algebraic  -set
-set
The set of solutions of a given system of algebraic equations. Let  be a field and let
be a field and let  be its algebraic closure. A subset
be its algebraic closure. A subset  of the Cartesian product
of the Cartesian product  is said to be an affine algebraic
is said to be an affine algebraic  -set if its points are the common zeros of some family
-set if its points are the common zeros of some family  of the ring of polynomials
of the ring of polynomials  . The set
. The set 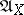 of all polynomials in
of all polynomials in  that vanish on
that vanish on 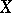 forms an ideal, the so-called ideal of the affine algebraic
forms an ideal, the so-called ideal of the affine algebraic  -set. The ideal
-set. The ideal 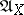 coincides with the radical of the ideal
coincides with the radical of the ideal  generated by the family
generated by the family  , i.e. with the set of polynomials
, i.e. with the set of polynomials 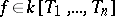 such that
such that 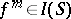 for some natural number
for some natural number  (Hilbert's Nullstellensatz; cf. Hilbert theorem 3)). Two affine algebraic sets
(Hilbert's Nullstellensatz; cf. Hilbert theorem 3)). Two affine algebraic sets  and
and  coincide if and only if
coincide if and only if  . The affine algebraic set
. The affine algebraic set  can be defined by a system of generators of
can be defined by a system of generators of 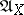 . In particular, any affine algebraic set can be defined by a finite number of polynomials
. In particular, any affine algebraic set can be defined by a finite number of polynomials  . The equalities
. The equalities  are called the equations of
are called the equations of  . The affine algebraic sets of
. The affine algebraic sets of  form a lattice with respect to the operations of intersection and union. The ideal of the intersection
form a lattice with respect to the operations of intersection and union. The ideal of the intersection  is identical with the sum of their ideals
is identical with the sum of their ideals  , while the ideal of the union
, while the ideal of the union  is identical with the intersection of their ideals
is identical with the intersection of their ideals  . Any set
. Any set  is an affine algebraic set, called an affine space over
is an affine algebraic set, called an affine space over  and denoted by
and denoted by  ; to it corresponds the zero ideal. The empty subset of
; to it corresponds the zero ideal. The empty subset of  is also an affine algebraic set with the unit ideal. The quotient ring
is also an affine algebraic set with the unit ideal. The quotient ring  is called the coordinate ring of
is called the coordinate ring of  . It is identical with the ring of
. It is identical with the ring of  -regular functions on
-regular functions on  , i.e. with the ring of
, i.e. with the ring of  -valued functions,
-valued functions,  , for which there exists a polynomial
, for which there exists a polynomial  such that
such that 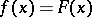 for all
for all  . An affine algebraic set is said to be irreducible if it is not the union of two affine algebraic proper subsets. An equivalent definition is that the ideal
. An affine algebraic set is said to be irreducible if it is not the union of two affine algebraic proper subsets. An equivalent definition is that the ideal 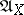 is prime. Irreducible affine algebraic sets together with projective algebraic sets were the subjects of classical algebraic geometry. They were called, respectively, affine algebraic varieties and projective algebraic varieties over the field
is prime. Irreducible affine algebraic sets together with projective algebraic sets were the subjects of classical algebraic geometry. They were called, respectively, affine algebraic varieties and projective algebraic varieties over the field  (or
(or 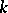 -varieties). Affine algebraic sets have the structure of a topological space. The affine algebraic subsets are the closed sets of this topology (the Zariski topology). An affine algebraic set is irreducible if and only if it is irreducible as a topological space. Further development of the concept of an affine algebraic set leads to the concepts of an affine variety and an affine scheme.
-varieties). Affine algebraic sets have the structure of a topological space. The affine algebraic subsets are the closed sets of this topology (the Zariski topology). An affine algebraic set is irreducible if and only if it is irreducible as a topological space. Further development of the concept of an affine algebraic set leads to the concepts of an affine variety and an affine scheme.
References
| [1] | O. Zariski, P. Samuel, "Commutative algebra" , 2 , Springer (1975) |
| [2] | I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) |
| [3] | R. Hartshorne, "Algebraic geometry" , Springer (1977) |
Comments
A topological space is irreducible if it is not the union of two closed proper subspaces.
Affine algebraic set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Affine_algebraic_set&oldid=13073