Aerodynamics, mathematical problems of
Problems involved in the solution of fundamental equations in aerodynamics, which are an accurate description of the laws of motion of a gas-like medium and its interaction forces with solids moving in this medium. Turbulence, for which no satisfactory mathematical model has yet been established, forms an exception to this rule. Processes without turbulence or in which the turbulence can be neglected may, in principle, be sufficiently completely investigated by a mathematical solution of the relevant equations. The real possibilities of solving such equations differ from the theoretical; accordingly, the orders of the individual terms in the equations are estimated, and on this basis simplified mathematical models are established for different classes of aerodynamic processes, in which one or more "small" terms in the complete set of aerodynamic equations are discarded. Even for such simplified models analytic solutions can be obtained only for the simplest cases, and numerical methods are widely employed in practical work in aerodynamics. These methods have become prevalent with the introduction of electronic computers.
As regards the nature of the equations involved in aerodynamical problems, these can be subdivided into four large classes.
1) Problems in the aerodynamics of an ideal (non-viscous and thermally non-conducting) fluid, the word "fluid" being used in this context to denote both liquids and gases.
2) Problems in the aerodynamics of viscous fluids.
3) Problems in the aerodynamics of radiant gases.
4) Problems in the aerodynamics of rarefied gases.
The equations of an ideal fluid are obtained from the general equations by making the Reynolds number — which describes the order of the ratio between the inertial and the viscous forces — grow without limit.
In most problems of applied aerodynamics of aircraft and rockets, and in seacraft hydrodynamics, the Reynolds numbers are very large (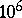 –
–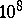 ), so that the model of an ideal fluid yields an accurate description of flow processes around solid bodies under these conditions, except for the boundary layer zone. The system of aerodynamic equations of an ideal fluid are:
), so that the model of an ideal fluid yields an accurate description of flow processes around solid bodies under these conditions, except for the boundary layer zone. The system of aerodynamic equations of an ideal fluid are:
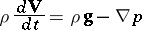 |
(equation of motion);
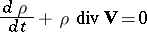 |
(continuity equation);
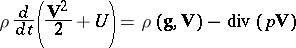 |
(equation of conservation of energy). Here 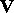 is the velocity vector,
is the velocity vector, 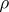 is the density,
is the density, 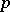 is the pressure,
is the pressure, 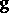 is the acceleration due to gravity and
is the acceleration due to gravity and 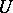 is the internal energy. It is a system of equations of the first order with respect to the functions sought. This is also true for a mixture of chemically interacting gases: The equations of the transfer of the mixture components are added to the above equations, while the heat generation due to chemical reactions is added to the energy equation.
is the internal energy. It is a system of equations of the first order with respect to the functions sought. This is also true for a mixture of chemically interacting gases: The equations of the transfer of the mixture components are added to the above equations, while the heat generation due to chemical reactions is added to the energy equation.
A number of simplified models can be derived from the model of an ideal fluid. The most important ones are the model of a weight-less fluid and the model of an incompressible fluid. The former model is the limiting case of the general model as the Froude number increases without limit; the Froude number describes the order of the ratio of the inertial to the gravity forces. This model is very accurate when applied to the aerodynamics of aircraft and rockets (with Froude numbers of order 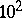 –
–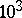 ). However, the force of gravity becomes significant in seacraft hydrodynamics and especially so in meteorological applications (with Froude number of order
). However, the force of gravity becomes significant in seacraft hydrodynamics and especially so in meteorological applications (with Froude number of order 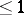 ).
).
The equation of an incompressible fluid is obtained from the general system by putting 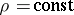 . This form of the equation of motion is obtained as the Mach number tends to zero (which is the relationship of the characteristic velocity of sound in a fluid medium). In the general case this is not true; it is only valid for Froude numbers
. This form of the equation of motion is obtained as the Mach number tends to zero (which is the relationship of the characteristic velocity of sound in a fluid medium). In the general case this is not true; it is only valid for Froude numbers 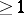 (i.e. if
(i.e. if 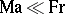 ), and also for quasi-stationary processes, in which the Strouhal number (the criterion of similitude of non-stationary motions of the liquid or the gas) is of order
), and also for quasi-stationary processes, in which the Strouhal number (the criterion of similitude of non-stationary motions of the liquid or the gas) is of order 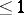 .
.
The simplest model is that of an incompressible fluid. In this model the entire system of equations is reduced to the single Laplace equation for the velocity potential 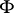 (
(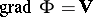 ). However, it is only in the case of plane-parallel motions of a weight-less fluid and axi-symmetric motion around solids of revolution that the solution of aerodynamic problems is reduced to problems in classical potential theory.
). However, it is only in the case of plane-parallel motions of a weight-less fluid and axi-symmetric motion around solids of revolution that the solution of aerodynamic problems is reduced to problems in classical potential theory.
The problem of flow around a given shape is solved by classical methods of the theory of conformal mapping. The flow around solids of revolution at zero angle of incidence is determined by the classical solution of the exterior Neumann problem for the Laplace equation. In view of the practical importance of these problems (determination of the characteristics of wing profiles and fuselages) many methods for their solutions have been developed that achieve an acceptable accuracy by means of relatively simple calculations. If electronic computers are employed, there is no point in using these methods, since accurate numerical methods for solving these problems belong to the simplest problems of computational mathematics.
In the spatial case the formal solution of the Neumann problem for the velocity potential will correspond to the physical picture of the flow only in very exceptional cases. In a viscous fluid a solid is followed by a turbulent trail. As the Reynolds number increases, this trail becomes thinner (for a continuous flow) and in the limit it becomes an infinitely thin turbulent surface, the intensity of the turbulent layer of which vanishes only in exceptional cases (e.g. in the case of plane-parallel motion). Accordingly, the problems involving discontinuous velocity potentials in the region of the flow zone represent the real spatial problems of an incompressible fluid. The location of this discontinuity surface is unknown, and for this reason the exact problem of flow around solid bodies in the presence of a discontinuous potential surface is a very complicated non-linear problem. It is only in the linear approximation, i.e. on the assumption that the solid around which the fluid is flowing disturbs the basic mainstream only to a small extent (a thin wing at a small angle of incidence) that the problem could be solved. In such a case the surface of turbulence can be considered as horizontal, and it may be assumed that the potential along the stream has a constant discontinuity. The normal derivatives of the velocity potential are given on the projection plane of the solid. Analytic solutions have been obtained on these assumptions (for a circular and an elliptic wing). Numerical methods of solving this problem for other shapes of wings are available and simplify the task to a considerable extent (cf. Wing theory).
The principal difficulty in problems involving a heavy fluid is that the boundary conditions for the potential on the free surface are non-linear. Exact solutions have been found for planar problems of the theory of waves only. Little progress has been made on the spatial problem of waves with a finite amplitude. On the other hand, the linearized problem (small wave amplitudes) has been largely solved, and the calculation of the wave resistance to the motion of a ship is actually based on the linear theory.
The possibility of aircraft travelling at near-sonic and supersonic speeds stimulated the search for solutions of aerodynamic problems of compressible fluids. The problems involving subsonic, transsonic and supersonic velocities are all treated in substantially different manners. In the subsonic range the aerodynamic equations remain elliptic and the solutions qualitatively resemble those obtained for incompressible fluids.
In the first period of research on the aerodynamics of compressible fluids much research was done on the effect of compressibility on the aerodynamic characteristics of the solids around which the flow takes place. All these methods involve some sort of linearization of the velocity of the unperturbed flow. Khristianovich's method is an exception, permitting as it does to obtain accurate solutions of the equations of subsonic aerodynamics, though for a solid whose shape is unknown in advance.
In practice, the difficulties involved in the problems of subsonic aerodynamics are the same as those to be dealt with when investigating incompressible fluids: problems involving plane-parallel and axi-symmetric flows may be fairly easily solved by numerical methods (cf. Integral-relation method; Adjustment method). In the case of spatial flows with discontinuous velocity potential, solutions can only be obtained for linearized equations. These equations can be converted, by an elementary transformation, into equations for incompressible fluids in which the boundary conditions and the conditions on the surface of discontinuity are the same as those for incompressible fluids.
The zone of transsonic aerodynamics is, from the point of view of mathematics, including numerical mathematics, the most difficult to study. The presence of local supersonic (parabolic) zones which almost always terminate in shock waves precludes any analytic approximation. Moreover, these problems display the principal drawback of equations of elliptic type — the propagation of the effect of any particular disturbance throughout the space. The most suitable method for solving the problems of transsonic aerodynamics is the adjustment method, in which a non-stationary aerodynamic problem is solved (starting from an arbitrary initial state), and the solution of the stationary problem of transsonic flow around a solid is obtained as a limit solution of the non-stationary problem as the time tends to infinity. This method is very laborious, but is quite feasible if electronic computers are employed.
As regards mathematical methods of study, supersonic aerodynamics may be subdivided into three fields.
1) Pure supersonic flow.
2) Mixed flow, with formation of local subsonic zones.
3) High-temperature hypersonic flow producing chemical reactions in the gas.
At higher velocities and, consequently, at higher temperatures ionization takes place and radiation processes become significant. This part of hypersonic aerodynamics may be said to form a separate field, since the mathematical problems involved are quite different from those arising in the case of "transparent" gases.
Problems in pure supersonic flow have been most thoroughly investigated. This included the development of numerical methods of characteristics, finite difference methods and methods of semi-characteristics, by which relatively simple solutions may be obtained not only for plane-parallel or axi-symmetric but also for spatial flows. The linear theory of supersonic flow has also been exhaustively studied. Analytic solutions can be obtained of numerous practical problems. The latter may be somewhat complicated by the occurrence of weak shock waves, but even these difficulties are of a computational and not of a principle character.
Practically speaking, these problems are limited to flows around sharply pointed solids and to the problems of internal aerodynamics (calculations of jet nozzles). However, if the supersonic velocities are very high, sharp-edged solids are not employed (charring of the edges), while a local subsonic flow always occurs at the blunt end. Having computed this region, the remaining (pure supersonic) flows are calculated by the methods of supersonic aerodynamics.
As compared with the aerodynamics of transsonic flow, the advantage of the problems of aerodynamics of supersonic flow with local subsonic zones (even though such zones are mixed) consists in the fact that such zones usually represent bounded narrow domains in the vicinity of the blunt ends. This is why it was possible to develop effective numerical methods for the computation of local subsonic zones (the method of integral relations, the method of inverse problems and the adjustment method). It should be noted, however, that up to the time of writing (1977) no rigorous mathematical investigations of these problems have ever been performed. There is also no proof that their solutions do exists and are unique. Accordingly, numerical methods are developed on the assumption that the conditions of continuous velocities and accelerations during the transition from the subsonic to the supersonic zone ensure the uniqueness of a solutions, which is physically realistic. This hypothesis is confirmed by all the results of numerical calculations.
Up till here, it has been said that the computation of the local subsonic zone (including the supersonic part of the region of influence) is followed by calculations of the flow by methods of purely supersonic aerodynamics.
There is another type of problems, which are connected with hypersonic flow around thin solids (prior to the initiation of chemical reactions). Hypersonic flows around thin solids (excepting the blunt-shaped regions) are distinguished by small changes in the velocity component along the main stream. For this reason the equations may be simplified so that the problem of flow around a thin body of a given shape (in the planar and axi-symmetric cases) becomes identical to the one-dimensional stationary problem. Many important qualitative characteristics of hypersonic flows have been obtained in this way and approximate similitude laws have been established; these are also extensively employed in the analysis of the results of numerical calculations, which are then reduced to very compact relations in a very wide range of Mach numbers and geometric parameters of the solid.
Aerodynamic problems concerned with gases undergoing chemical reactions involve the simultaneous solution of the equations of motion and the equations of chemical kinetics. While the resulting systems of equations are more complicated, the numerical methods employed in their solution are essentially the same as those employed in the aerodynamics of an ideal gas, except that they are much more laborious. Such calculations are extensively carried out in practical work, and since modelling natural conditions in aerodynamic tubes cannot be realized in this temperature range, the aerodynamic characteristics of hypersonic instruments are mainly obtained by numerical methods.
There are two principal trends in the theory of viscous fluids — the theory of the complete equations of a viscous fluid (Navier–Stokes equations), and boundary-layer theory. The boundary-layer equations represent the principal term of the asymptotic expansion of the Navier–Stokes equations in the vicinity of the boundary of the solid to which the fluid particles adhere, completely or in part. It is this fact which radically disturbs the solutions obtained for ideal fluids near the surface of the solid around which the flow takes place. The order of the error involved in the boundary-layer equations is 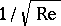 , which means that the theory is valid for large Reynolds numbers only, and even then only in the regions of smooth continuous flow. Despite the fact that the boundary-layer equations contain all the main terms of viscous stresses, their mathematical structure is much simpler. While the complete equations are of elliptic type, the boundary-layer equations are parabolic with characteristics directed along the normal to the surface of the solid. It is therefore possible to conduct the computations "layer by layer" , i.e. to pass from one section of the boundary layer to another, irrespective of the conditions prevailing outside the range between the sections.
, which means that the theory is valid for large Reynolds numbers only, and even then only in the regions of smooth continuous flow. Despite the fact that the boundary-layer equations contain all the main terms of viscous stresses, their mathematical structure is much simpler. While the complete equations are of elliptic type, the boundary-layer equations are parabolic with characteristics directed along the normal to the surface of the solid. It is therefore possible to conduct the computations "layer by layer" , i.e. to pass from one section of the boundary layer to another, irrespective of the conditions prevailing outside the range between the sections.
One consequence of the practical importance of the theory of boundary layers (computations of the resistance, of the surface temperatures, of the rate of destroyment of the surface under hypersonic flight conditions) was the development of numerous approximate methods for performing such calculations (the Pohlhausen method, the one-parameter Kochin–Loitsyanskii method, etc.). However, if electronic computers are employed, all these approximate methods become superfluous, since an accurate numerical solution of the boundary-layer equations presents no difficulties, even in the difficult case of a hot gas in which chemical reactions are taking place. The numerical routines may be so constructed that at each step the system of equations is split, with respect to the  -variable (along the tangent to the surface of the solid), into a number of separate second-order differential equations which, from the computational point of view, is highly advantageous.
-variable (along the tangent to the surface of the solid), into a number of separate second-order differential equations which, from the computational point of view, is highly advantageous.
What was said above applies to plane-parallel and to axi-symmetric flows. The structure of three-dimensional boundary layers is more complicated. The equations of the three-dimensional layers themselves vary significantly with the geometry of the solid around which the flow takes place. The development of methods of calculation of three-dimensional boundary layers is much less advanced, partly because calculations on plane sections are often used in practice; this, despite the lack of a theoretical basis, often yields sufficiently accurate results. There are no principal difficulties in solving the exact equations of a three-dimensional layer.
Except for a few special cases, in which analytic solutions could be obtained, the development of methods for solving the complete system of equations for a viscous liquid is due to the introduction of electronic computers. The principal difficulty in solving such equations is their high order and the fact that the region of influence is unbounded. In the simplest case of stationary motion of a viscous incompressible fluid with a constant viscosity coefficient one obtains a system of two equations of the second order with respect to the stream function 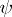 and vortex velocity
and vortex velocity 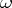 . They may be written in the dimension-less form as follows:
. They may be written in the dimension-less form as follows:
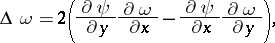 |
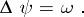 |
The boundary conditions on solid boundaries are only for the stream function 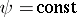 ,
, 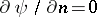 . The solution of this non-linear system of the fourth order can only be obtained by some kind of iterative process. The iterative process is so constructed that separate equations for the vortex velocity and for the flow function are obtained at each iteration step. Such a separation must take place not only in the equations, but in the boundary conditions as well. Thus, by choosing the solution of the ideal fluid equations as the first approximation, one obtains the following set of iterations:
. The solution of this non-linear system of the fourth order can only be obtained by some kind of iterative process. The iterative process is so constructed that separate equations for the vortex velocity and for the flow function are obtained at each iteration step. Such a separation must take place not only in the equations, but in the boundary conditions as well. Thus, by choosing the solution of the ideal fluid equations as the first approximation, one obtains the following set of iterations:
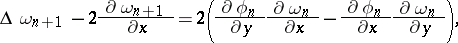 |
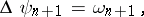 |
with the following boundary conditions on the solid boundaries:
 |
where 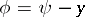 , which means that a separate set of equations for the vortex flow and the flow function is thus obtained in the (
, which means that a separate set of equations for the vortex flow and the flow function is thus obtained in the (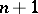 )-st approximation. The solution may be obtained in a similar manner by the adjustment method, but it is not necessary in such a case to take a real system of non-stationary equations; rather, one may consider the system of parabolic equations:
)-st approximation. The solution may be obtained in a similar manner by the adjustment method, but it is not necessary in such a case to take a real system of non-stationary equations; rather, one may consider the system of parabolic equations:
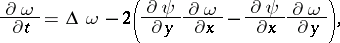 |
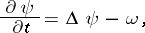 |
which is more convenient to handle in numerical calculations.
The problem of flow around a body by a viscous fluid involves not merely the development of computation methods, but also research on fundamental questions. Thus, it is unclear whether a stationary solution exists at large Reynolds numbers (e.g. for the case of flow around a cylinder). Numerical methods yield acceptable solutions up to Reynolds numbers of several hundreds, but above these values of the Reynolds number the numerical calculations no longer converge.
Problems in the aerodynamics of radiant gases and of rarefied gases have been solved only for the simplest cases. However, in view of the practical importance of these problems (in both these fields), mathematical models of the relevant phenomena have been proposed. Such models very often are no limiting cases of the complete equations (model of gray radiation, model of diffusive radiation in the theory of radiant gases, Crook's model in the theory of rarefied gases), but merely qualitative reflections of the relationships described in the complete equations. The volume of the computations involved in solving these problems is very large, and success in this field will depend on the possibilities for increasing the effectiveness of electronic computers.
References
| [1] | N.E. Kochin, I.A. Kibel', N.V. Roze, "Theoretical hydrodynamics" , Interscience (1964) (Translated from Russian) |
| [2] | S.A. Khristianovich, "Gas flow around bodies with large subsonic speed" , Moscow (1940) (In Russian) |
| [3] | L.J. [L.I. Sedov] Sedov, "Two-dimensional problems in hydrodynamics and aerodynamics" , Acad. Press (1965) (Translated from Russian) |
| [4] | W. Hayes, "Hypersonic flow theory" , Acad. Press (1966) |
| [5] | G.G. Chernyi, "Gas flow with large supersonic speed" , Moscow (1959) (In Russian) |
| [6] | O.M. Belotserkovskii, P.I. Chushkin, "The numerical solution of problems in gas dynamics" , Basic developments in fluid dynamics , 1 , Acad. Press (1965) pp. 1–126 |
| [7] | P.I. Chushkin, "The method of characteristics for spatial supersonic flows" , Moscow (1968) (In Russian) |
| [8] | , Flow around blunted bodies of a supersonic gas flow , Moscow (1967) (In Russian) |
| [9] | , Numerical methods in fluid mechanics , Wroclaw (1969) (In Polish) |
Comments
In the equation of the conservation of energy 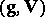 denotes the scalar product of two vectors.
denotes the scalar product of two vectors.
For some material on the branch or aerodynamics dealing with such things as plasmas and the mechanics of stellar gases (magneto- and electro-aerodynamics) see the article Magneto-hydrodynamics, mathematical problems in.
References
| [a1] | G.K. Bachelor, "An introduction to fluid dynamics" , Cambridge Univ. Press (1970) |
| [a2] | S.I. Pai, "Viscous flow" , 1–2 , v. Nostrand (1956) |
| [a3] | L. Howarth (ed.) , Modern development in fluid dynamics. High speed flow , 1–2 , Oxford Univ. Press (1953) |
| [a4] | G. Birhoff, "Hydrodynamics, a study in logic, fact and similitude" , Princeton Univ. Press (1960) |
| [a5] | Th. von Kármán (ed.) et al. (ed.) , High speed aerodynamics and jet propulsion , 1–2 , Princeton Univ. Press (1964) |
| [a6] | S.I. Pai, "Radiation gas dynamics" , Springer (1966) |
| [a7] | V.C.A. Ferraro, C. Plumpton, "An introduction to magneto-fluid mechanics" , Oxford Univ. Press (1966) |
| [a8] | M.V. Kogan, "Rarified gas dynamics" , Acad. Press (1969) (Translated from Russian) |
| [a9] | L. Bers, "Mathematical aspects of subsonic and transonic gas dynamics" , Wiley (1958) |
Aerodynamics, mathematical problems of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Aerodynamics,_mathematical_problems_of&oldid=28149