Adjoint functor
A concept expressing the universality and naturalness of many important mathematical constructions, such as a free universal algebra, various completions, and direct and inverse limits.
Let 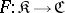 be a covariant functor in one argument from a category
be a covariant functor in one argument from a category 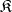 into a category
into a category 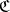 .
. 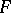 induces a functor
induces a functor
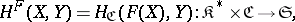 |
where 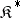 is the category dual to
is the category dual to 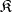 ,
,  is the category of sets, and
is the category of sets, and 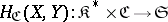 is the basic set-valued functor. The functor
is the basic set-valued functor. The functor  is contravariant in the first argument and covariant in the second. Similarly, any covariant functor
is contravariant in the first argument and covariant in the second. Similarly, any covariant functor 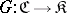 induces a functor
induces a functor
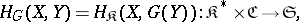 |
which is also contravariant in the first argument and covariant in the second. The functors 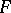 and
and 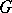 are adjoint, or form an adjoint pair, if
are adjoint, or form an adjoint pair, if 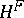 and
and 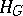 are isomorphic, that is, if there is a natural transformation
are isomorphic, that is, if there is a natural transformation 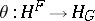 that establishes a one-to-one correspondence between the sets of morphisms
that establishes a one-to-one correspondence between the sets of morphisms 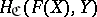 and
and 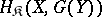 for all objects
for all objects 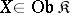 and
and 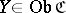 . The transformation
. The transformation 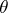 is called the adjunction of
is called the adjunction of 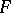 with
with 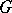 ,
, 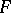 is called the left adjoint of
is called the left adjoint of  and
and 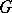 the right adjoint of
the right adjoint of 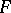 (this is written
(this is written 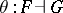 , or simply
, or simply 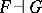 ). The transformation
). The transformation 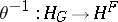 is called the co-adjunction.
is called the co-adjunction.
Let 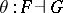 . For all
. For all 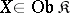 and
and 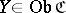 , let
, let
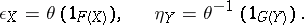 |
The families of morphisms 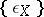 and
and 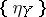 define natural transformations
define natural transformations 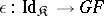 and
and 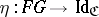 , called the unit and co-unit of the adjunction
, called the unit and co-unit of the adjunction 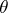 . They satisfy the following equations:
. They satisfy the following equations:
 |
In general, a pair of natural transformations 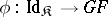 and
and 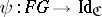 leads to an adjoint pair (or adjunction) if the following equations hold:
leads to an adjoint pair (or adjunction) if the following equations hold:
 |
for all objects 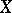 and
and 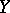 . A natural transformation
. A natural transformation 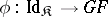 is the unit of some adjunction if and only if for any morphism
is the unit of some adjunction if and only if for any morphism 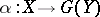 in
in 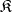 there is a unique morphism
there is a unique morphism 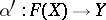 in
in 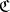 such that
such that 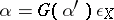 . This property expresses the fact that
. This property expresses the fact that  is a free object over
is a free object over 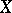 with respect to the functor
with respect to the functor 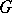 in the sense of the following definition. An object
in the sense of the following definition. An object 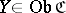 together with a morphism
together with a morphism  is free over an object
is free over an object 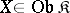 if every morphism
if every morphism 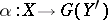 can be written uniquely in the form
can be written uniquely in the form 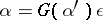 for some morphism
for some morphism 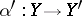 . A functor
. A functor 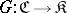 has a left adjoint if and only if for every
has a left adjoint if and only if for every 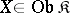 there is an object
there is an object 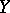 that is free over
that is free over 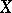 with respect to
with respect to 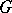 .
.
Examples of adjoint functors.
1) If 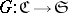 , where
, where 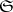 is the category of sets, then
is the category of sets, then 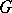 has a left adjoint only if it is representable. A representable functor
has a left adjoint only if it is representable. A representable functor 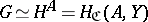 has a left adjoint if and only if all co-products
has a left adjoint if and only if all co-products 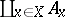 exist in
exist in 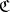 , where
, where 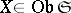 and
and  for all
for all 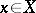 .
.
2) In the category 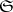 of sets, for any set
of sets, for any set 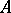 the basic functor
the basic functor 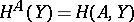 is the right adjoint of the functor
is the right adjoint of the functor  .
.
3) In the category of Abelian groups, the functor 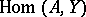 is the right adjoint of the functor
is the right adjoint of the functor 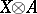 of tensor multiplication by
of tensor multiplication by  , and the imbedding functor of the full subcategory of torsion groups is the left adjoint of the functor of taking the torsion part of any Abelian group.
, and the imbedding functor of the full subcategory of torsion groups is the left adjoint of the functor of taking the torsion part of any Abelian group.
4) Let 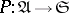 be the forgetful functor from an arbitrary variety of universal algebras into the category of sets. The functor
be the forgetful functor from an arbitrary variety of universal algebras into the category of sets. The functor 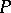 has a left adjoint
has a left adjoint 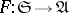 , which assigns to every set
, which assigns to every set 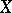 the free algebra of the variety
the free algebra of the variety  with
with 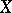 as set of free generators.
as set of free generators.
5) The imbedding functor 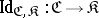 of an arbitrary reflective subcategory
of an arbitrary reflective subcategory 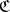 of a category
of a category 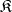 is the right adjoint of the
is the right adjoint of the 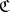 -reflector (cf. also Reflexive subcategor). In particular, the imbedding functor of the category of Abelian groups in the category of groups has a left adjoint, which assigns to every group
-reflector (cf. also Reflexive subcategor). In particular, the imbedding functor of the category of Abelian groups in the category of groups has a left adjoint, which assigns to every group 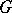 its quotient group by the commutator subgroup.
its quotient group by the commutator subgroup.
Properties of adjoint functors.
The left adjoint functor of a given functor is uniquely determined up to isomorphism of functors. Left adjoints commute with co-limits (e.g. co-products) and send null objects and null morphism into null objects and null morphisms, respectively.
Let 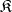 and
and 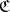 be categories that are complete on the left and locally small on the left. A functor
be categories that are complete on the left and locally small on the left. A functor 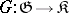 has a left adjoint
has a left adjoint 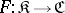 if and only if the following conditions hold: a)
if and only if the following conditions hold: a)  commutes with limits; b) for every
commutes with limits; b) for every 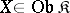 , at least one of the sets
, at least one of the sets 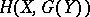 ,
, 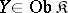 , is non-empty; and c) for every
, is non-empty; and c) for every 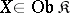 , there is a set
, there is a set 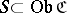 such that every morphism
such that every morphism 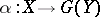 is representable in the form
is representable in the form 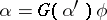 , where
, where 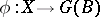 ,
, 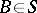 ,
, 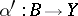 .
.
By passing to dual categories, one may establish a duality between the concepts of a "left adjoint functor" and a "right adjoint functor" ; this enables one to deduce the properties of right adjoints from those of left adjoints.
The concept of an adjoint functor is directly connected with the concept of a triple (or monad) in a category.
References
| [1] | M.Sh. Tsalenko, E.G. Shul'geifer, "Fundamentals of category theory" , Moscow (1974) (In Russian) |
| [2] | S. Maclane, "Categories for the working mathematician" , Springer (1971) |
Comments
A category is called complete on the left if small diagrams have limits. A category is called locally small on the left if it has small hom-sets. The statement that a functor has a left adjoint if and only if a), b) and c) above holds, is called the Freyd adjoint functor theorem.
Adjoint functor. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Adjoint_functor&oldid=16692