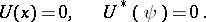to an ordinary linear differential equation 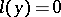
The ordinary linear differential equation 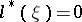 , where
, where
 | (1) |
 is the space of
is the space of 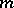 -times continuously-differentiable complex-valued functions on
-times continuously-differentiable complex-valued functions on 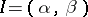 , and
, and
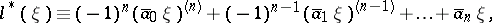 | (2) |
(the bar denotes complex conjugation). It follows at once that
for any scalar 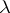 . The adjoint of the equation
. The adjoint of the equation 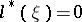 is
is 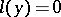 . For all
. For all  -times continuously-differentiable functions
-times continuously-differentiable functions 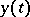 and
and 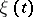 , Lagrange's identity holds:
, Lagrange's identity holds:
It implies Green's formula
If 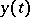 and
and  are arbitrary solutions of
are arbitrary solutions of  and
and  , respectively, then
, respectively, then
A knowledge of  linearly independent solutions of the equation
linearly independent solutions of the equation 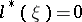 enables one to reduce the order of the equation
enables one to reduce the order of the equation 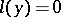 by
by 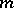 (see [1]–[3]).
(see [1]–[3]).
For a system of differential equations
where 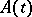 is a continuous complex-valued
is a continuous complex-valued 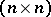 -matrix, the adjoint system is given by
-matrix, the adjoint system is given by
(see [1], [4]), where 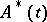 is the Hermitian adjoint of
is the Hermitian adjoint of 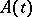 . The Lagrange identity and the Green formula take the form
. The Lagrange identity and the Green formula take the form
where 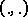 is the standard scalar product (the sum of the products of coordinates with equal indices). If
is the standard scalar product (the sum of the products of coordinates with equal indices). If 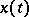 and
and 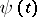 are arbitrary solutions of the equations
are arbitrary solutions of the equations 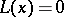 and
and 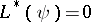 , then
, then
The concept of an adjoint differential equation is closely connected with the general concept of an adjoint operator. Thus, if 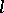 is a linear differential operator acting on
is a linear differential operator acting on 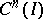 into
into 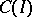 in accordance with (1), then its adjoint differential operator
in accordance with (1), then its adjoint differential operator 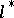 maps the space
maps the space 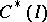 adjoint to
adjoint to 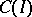 into the space
into the space 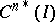 adjoint to
adjoint to 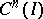 . The restriction of
. The restriction of 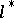 to
to 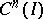 is given by formula (2) (see [5]).
is given by formula (2) (see [5]).
Adjoints are also defined for linear partial differential equations (see [6], [5]).
Let 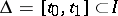 , and let
, and let 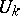 be linearly independent linear functionals on
be linearly independent linear functionals on 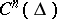 . Then the boundary value problem adjoint to the linear boundary value problem
. Then the boundary value problem adjoint to the linear boundary value problem
 | (3) |
is defined by the equations
 | (4) |
Here the 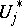 are linear functionals on
are linear functionals on 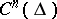 describing the adjoint boundary conditions, that is, they are defined in such a way that the equation (see Green formulas)
describing the adjoint boundary conditions, that is, they are defined in such a way that the equation (see Green formulas)
holds for any pair of functions 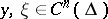 that satisfy the conditions
that satisfy the conditions 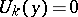 ,
, 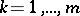 ;
;  ,
,  .
.
If
are linear forms in the variables
then 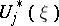 are linear forms in the variables
are linear forms in the variables
Examples. For the problem
with real 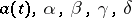 , the adjoint boundary value problem has the form
, the adjoint boundary value problem has the form
If problem (3) has 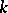 linearly independent solutions (in this case the rank
linearly independent solutions (in this case the rank  of the boundary value problem is equal to
of the boundary value problem is equal to 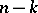 ), then problem (4) has
), then problem (4) has 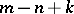 linearly independent solutions (its rank is
linearly independent solutions (its rank is 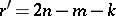 ). When
). When  , problems (3) and (4) have an equal number of linearly independent solutions. Therefore, when
, problems (3) and (4) have an equal number of linearly independent solutions. Therefore, when  , problem (3) has only a trivial solution if and only if the adjoint boundary value problem (4) has the same property. The Fredholm alternative holds: The semi-homogeneous boundary value problem
, problem (3) has only a trivial solution if and only if the adjoint boundary value problem (4) has the same property. The Fredholm alternative holds: The semi-homogeneous boundary value problem
has a solution if 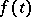 is orthogonal to all non-trivial solutions
is orthogonal to all non-trivial solutions 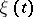 of the adjoint boundary value problem (4), i.e. if
of the adjoint boundary value problem (4), i.e. if
(see [1]–[3], [7]).
For the eigen value problem
 | (5) |
the adjoint eigen value problem is defined as
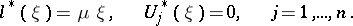 | (6) |
If 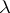 is an eigen value of (5), then
is an eigen value of (5), then 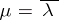 is an eigen value of (6). The eigen functions
is an eigen value of (6). The eigen functions 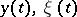 corresponding to eigen values
corresponding to eigen values 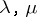 of (5), (6), respectively, are orthogonal if
of (5), (6), respectively, are orthogonal if 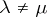 (see [1]–[3]):
(see [1]–[3]):
For the linear boundary value problem
 | (7) |
where 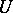 is an
is an 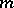 -dimensional vector functional on the space
-dimensional vector functional on the space 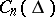 of continuously-differentiable complex-valued
of continuously-differentiable complex-valued  -dimensional vector functions with
-dimensional vector functions with 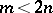 , the adjoint boundary value problem is defined by
, the adjoint boundary value problem is defined by
 | (8) |
(see [1]). Here 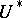 is a
is a 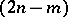 -dimensional vector functional defined such that the equation
-dimensional vector functional defined such that the equation
holds for any pair of functions 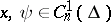 satisfying the conditions
satisfying the conditions
The problems (7), (8) possess properties analogous to those listed above (see [1]).
The concept of an adjoint boundary value problem is closely connected with that of an adjoint operator [5]. Adjoint boundary value problems are also defined for linear boundary value problems for partial differential equations (see [6], [7]).
References
| [1] | E. Kamke, "Differentialgleichungen: Lösungen und Lösungsmethoden" , 1. Gewöhnliche Differentialgleichungen , Chelsea, reprint (1971) |
| [2] | M.A. Naimark, "Linear differential operators" , 1–2 , F. Ungar (1967–1968) (Translated from Russian) |
| [3] | E.A. Coddington, N. Levinson, "Theory of ordinary differential equations" , McGraw-Hill (1955) pp. Chapts. 13–17 |
| [4] | P. Hartman, "Ordinary differential equations" , Birkhäuser (1982) |
| [5] | N. Dunford, J.T. Schwartz, "Linear operators. Spectral theory" , 2 , Interscience (1963) |
| [6] | V.P. Mikhailov, "Partial differential equations" , MIR (1978) (Translated from Russian) |
| [7] | V.S. Vladimirov, "Gleichungen der mathematischen Physik" , MIR (1984) (Translated from Russian) |
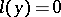
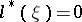 , where
, where

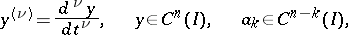
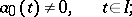
 is the space of
is the space of 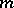 -times continuously-differentiable complex-valued functions on
-times continuously-differentiable complex-valued functions on 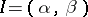 , and
, and
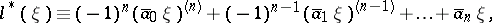
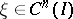
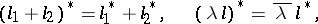
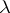 . The adjoint of the equation
. The adjoint of the equation 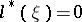 is
is 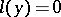 . For all
. For all  -times continuously-differentiable functions
-times continuously-differentiable functions 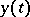 and
and 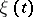 , Lagrange's identity holds:
, Lagrange's identity holds:
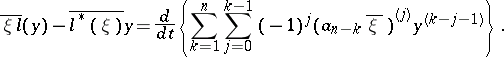
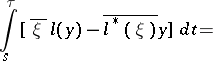
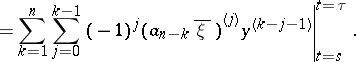
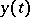 and
and  are arbitrary solutions of
are arbitrary solutions of  and
and  , respectively, then
, respectively, then
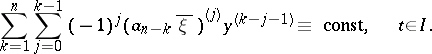
 linearly independent solutions of the equation
linearly independent solutions of the equation 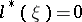 enables one to reduce the order of the equation
enables one to reduce the order of the equation 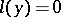 by
by 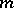 (see [1]–[3]).
(see [1]–[3]).
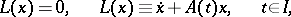
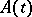 is a continuous complex-valued
is a continuous complex-valued 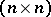 -matrix, the adjoint system is given by
-matrix, the adjoint system is given by
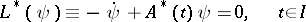
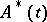 is the Hermitian adjoint of
is the Hermitian adjoint of 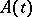 . The Lagrange identity and the Green formula take the form
. The Lagrange identity and the Green formula take the form
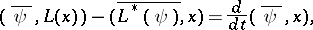
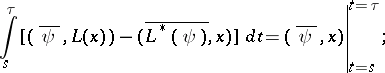
 is the standard scalar product (the sum of the products of coordinates with equal indices). If
is the standard scalar product (the sum of the products of coordinates with equal indices). If 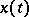 and
and 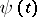 are arbitrary solutions of the equations
are arbitrary solutions of the equations 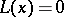 and
and 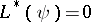 , then
, then
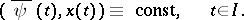
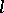 is a linear differential operator acting on
is a linear differential operator acting on 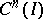 into
into 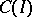 in accordance with (1), then its adjoint differential operator
in accordance with (1), then its adjoint differential operator 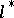 maps the space
maps the space 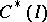 adjoint to
adjoint to 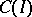 into the space
into the space 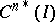 adjoint to
adjoint to 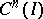 . The restriction of
. The restriction of 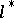 to
to 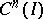 is given by formula (2) (see [5]).
is given by formula (2) (see [5]).
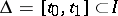 , and let
, and let 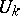 be linearly independent linear functionals on
be linearly independent linear functionals on 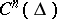 . Then the boundary value problem adjoint to the linear boundary value problem
. Then the boundary value problem adjoint to the linear boundary value problem


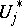 are linear functionals on
are linear functionals on 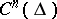 describing the adjoint boundary conditions, that is, they are defined in such a way that the equation (see Green formulas)
describing the adjoint boundary conditions, that is, they are defined in such a way that the equation (see Green formulas)

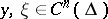 that satisfy the conditions
that satisfy the conditions 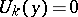 ,
, 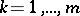 ;
;  ,
,  .
.
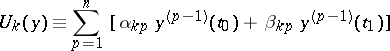
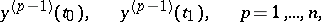
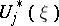 are linear forms in the variables
are linear forms in the variables
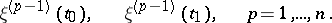
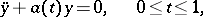
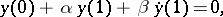
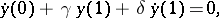
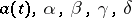 , the adjoint boundary value problem has the form
, the adjoint boundary value problem has the form
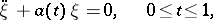
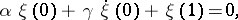
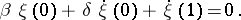
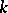 linearly independent solutions (in this case the rank
linearly independent solutions (in this case the rank  of the boundary value problem is equal to
of the boundary value problem is equal to 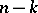 ), then problem (4) has
), then problem (4) has 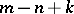 linearly independent solutions (its rank is
linearly independent solutions (its rank is 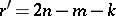 ). When
). When  , problems (3) and (4) have an equal number of linearly independent solutions. Therefore, when
, problems (3) and (4) have an equal number of linearly independent solutions. Therefore, when  , problem (3) has only a trivial solution if and only if the adjoint boundary value problem (4) has the same property. The Fredholm alternative holds: The semi-homogeneous boundary value problem
, problem (3) has only a trivial solution if and only if the adjoint boundary value problem (4) has the same property. The Fredholm alternative holds: The semi-homogeneous boundary value problem
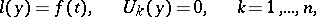
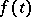 is orthogonal to all non-trivial solutions
is orthogonal to all non-trivial solutions 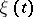 of the adjoint boundary value problem (4), i.e. if
of the adjoint boundary value problem (4), i.e. if
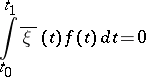

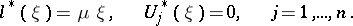
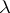 is an eigen value of (5), then
is an eigen value of (5), then 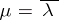 is an eigen value of (6). The eigen functions
is an eigen value of (6). The eigen functions 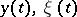 corresponding to eigen values
corresponding to eigen values 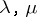 of (5), (6), respectively, are orthogonal if
of (5), (6), respectively, are orthogonal if 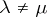 (see [1]–[3]):
(see [1]–[3]):
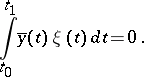

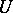 is an
is an 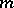 -dimensional vector functional on the space
-dimensional vector functional on the space 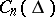 of continuously-differentiable complex-valued
of continuously-differentiable complex-valued  -dimensional vector functions with
-dimensional vector functions with 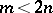 , the adjoint boundary value problem is defined by
, the adjoint boundary value problem is defined by

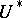 is a
is a 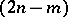 -dimensional vector functional defined such that the equation
-dimensional vector functional defined such that the equation
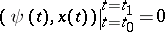
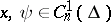 satisfying the conditions
satisfying the conditions