Linear connections  and
and  such that for the corresponding operators of covariant differentiation
such that for the corresponding operators of covariant differentiation  and
and  there holds
there holds
where  and
and  are arbitrary vector fields,
are arbitrary vector fields, 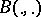 is a quadratic form (i.e. a symmetric bilinear form), and
is a quadratic form (i.e. a symmetric bilinear form), and 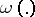 is a
is a  -form (or covector field). One also says that
-form (or covector field). One also says that  and
and  are adjoint with respect to
are adjoint with respect to 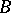 . In coordinate form (where
. In coordinate form (where 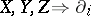 ,
, 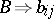 ,
, 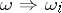 ,
, 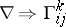 ),
),
For the curvature operators 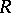 and
and 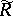 and torsion operators
and torsion operators 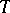 and
and 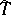 of the connections
of the connections  and
and  , respectively, the following relations hold:
, respectively, the following relations hold:
In coordinate form,
References
| [1] | A.P. Norden, "Spaces with an affine connection" , Nauka , Moscow-Leningrad (1976) (In Russian) |
Instead of the name adjoint connections one also encounters conjugate connections.
Sometimes the  -form
-form 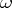 is not mentioned in the notion of adjoint connections. Strictly speaking this notion of an "adjoint connection" should be called "adjoint with respect to B and w" .
is not mentioned in the notion of adjoint connections. Strictly speaking this notion of an "adjoint connection" should be called "adjoint with respect to B and w" .
How to Cite This Entry:
Adjoint connections. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Adjoint_connections&oldid=18145
This article was adapted from an original article by M.I. Voitsekhovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article and
and  such that for the corresponding operators of covariant differentiation
such that for the corresponding operators of covariant differentiation  and
and  there holds
there holds

 and
and  are arbitrary vector fields,
are arbitrary vector fields, 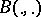 is a quadratic form (i.e. a symmetric bilinear form), and
is a quadratic form (i.e. a symmetric bilinear form), and 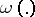 is a
is a  -form (or covector field). One also says that
-form (or covector field). One also says that  and
and  are adjoint with respect to
are adjoint with respect to 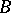 . In coordinate form (where
. In coordinate form (where 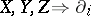 ,
, 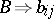 ,
, 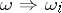 ,
, 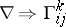 ),
),
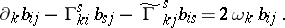
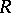 and
and 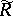 and torsion operators
and torsion operators 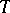 and
and 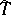 of the connections
of the connections  and
and  , respectively, the following relations hold:
, respectively, the following relations hold:
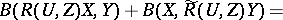
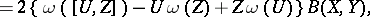
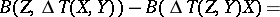
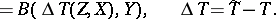

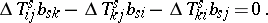
 -form
-form  is not mentioned in the notion of adjoint connections. Strictly speaking this notion of an "adjoint connection" should be called "adjoint with respect to B and w" .
is not mentioned in the notion of adjoint connections. Strictly speaking this notion of an "adjoint connection" should be called "adjoint with respect to B and w" .