Adic topology
A linear topology of a ring 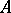 in which the fundamental system of neighbourhoods of zero consists of the powers
in which the fundamental system of neighbourhoods of zero consists of the powers 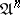 of some two-sided ideal
of some two-sided ideal 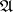 . The topology is then said to be
. The topology is then said to be 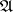 -adic, and the ideal
-adic, and the ideal 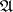 is said to be the defining ideal of the topology. The closure of any set
is said to be the defining ideal of the topology. The closure of any set 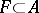 in the
in the 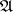 -adic topology is equal to
-adic topology is equal to 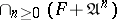 ; in particular, the topology is separable if, and only if,
; in particular, the topology is separable if, and only if, 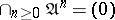 . The separable completion
. The separable completion 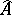 of the ring
of the ring 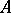 in an
in an 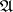 -adic topology is isomorphic to the projective limit
-adic topology is isomorphic to the projective limit 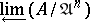 .
.
The 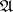 -adic topology of an
-adic topology of an 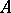 -module
-module 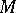 is defined in a similar manner: its fundamental system of neighbourhoods of zero is given by the submodules
is defined in a similar manner: its fundamental system of neighbourhoods of zero is given by the submodules 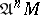 ; in the
; in the 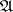 -adic topology
-adic topology 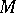 becomes a topological
becomes a topological 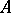 -module.
-module.
Let 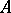 be a commutative ring with identity with an
be a commutative ring with identity with an 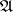 -adic topology and let
-adic topology and let 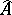 be its completion; if
be its completion; if 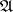 is an ideal of finite type, the topology in
is an ideal of finite type, the topology in 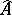 is
is 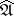 -adic, and
-adic, and 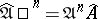 . If
. If 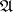 is a maximal ideal, then
is a maximal ideal, then 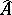 is a local ring with maximal ideal
is a local ring with maximal ideal 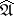 . A local ring topology is an adic topology defined by its maximal ideal (an
. A local ring topology is an adic topology defined by its maximal ideal (an  -adic topology).
-adic topology).
A fundamental tool in the study of adic topologies of rings is the Artin–Rees lemma: Let 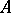 be a commutative Noetherian ring, let
be a commutative Noetherian ring, let 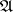 be an ideal in
be an ideal in 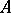 , let
, let 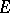 be an
be an 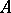 -module of finite type, and let
-module of finite type, and let 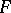 be a submodule of
be a submodule of 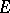 . Then there exists a
. Then there exists a 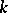 such that, for any
such that, for any 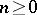 , the following equality is valid:
, the following equality is valid:
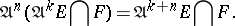 |
The topological interpretation of the Artin–Rees lemma shows that the 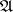 -adic topology of
-adic topology of 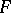 is induced by the
is induced by the 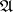 -adic topology of
-adic topology of 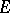 . It follows that the completion
. It follows that the completion 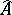 of a ring
of a ring 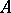 in the
in the 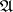 -adic topology is a flat
-adic topology is a flat 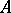 -module (cf. Flat module), that the completion
-module (cf. Flat module), that the completion 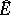 of the
of the 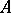 -module
-module 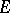 of finite type is identical with
of finite type is identical with  , and that Krull's theorem holds: The
, and that Krull's theorem holds: The 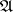 -adic topology of a Noetherian ring is separable if and only if the set
-adic topology of a Noetherian ring is separable if and only if the set 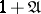 contains no zero divisors. In particular, the topology is separable if
contains no zero divisors. In particular, the topology is separable if 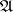 is contained in the (Jacobson) radical of the ring.
is contained in the (Jacobson) radical of the ring.
References
| [1] | O. Zariski, P. Samuel, "Commutative algebra" , 2 , Springer (1975) |
| [2] | N. Bourbaki, "Elements of mathematics. Commutative algebra" , Addison-Wesley (1972) (Translated from French) |
Adic topology. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Adic_topology&oldid=16092