Adele group
An element of the adèle group, i.e. of the restricted topological direct product
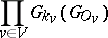 |
of the group 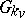 with distinguished invariant open subgroups
with distinguished invariant open subgroups  . Here
. Here 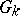 is a linear algebraic group, defined over a global field
is a linear algebraic group, defined over a global field 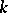 ,
, 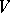 is the set of valuations (cf. Valuation) of
is the set of valuations (cf. Valuation) of  ,
, 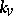 is the completion of
is the completion of 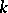 with respect to
with respect to 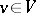 , and
, and 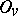 is the ring of integer elements in
is the ring of integer elements in 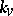 . The adèle group of an algebraic group
. The adèle group of an algebraic group 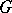 is denoted by
is denoted by 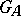 . Since all groups
. Since all groups 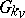 are locally compact and since
are locally compact and since 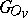 is compact,
is compact, 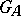 is a locally compact group.
is a locally compact group.
Examples. 1) If 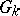 is the additive group
is the additive group 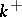 of the field
of the field 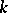 , then
, then 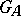 has a natural ring structure, and is called the adèle ring of
has a natural ring structure, and is called the adèle ring of 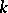 ; it is denoted by
; it is denoted by 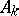 . 2) If
. 2) If 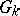 is the multiplicative group
is the multiplicative group 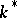 of the field
of the field 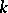 , then
, then 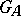 is called the idèle group of
is called the idèle group of 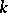 (the idèle group is the group of units in the adèle ring
(the idèle group is the group of units in the adèle ring 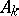 ). 3) If
). 3) If 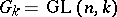 is the general linear group over
is the general linear group over 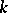 , then
, then 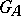 consists of the elements
consists of the elements 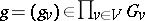 for which
for which 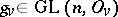 for almost all valuations
for almost all valuations  .
.
The concept of an adèle group was first introduced by C. Chevalley (in the 1930s) for algebraic number fields, to meet certain needs of class field theory. It was generalized twenty years later to algebraic groups by M. Kneser and T. Tamagawa [1], . They noted that the principal results on the arithmetic of quadratic forms over number fields can be conveniently reformulated in terms of adèle groups.
The image of the diagonal imbedding of 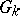 in
in 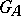 is a discrete subgroup in
is a discrete subgroup in 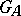 , called the subgroup of principal adèles. If
, called the subgroup of principal adèles. If 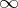 is the set of all Archimedean valuations of
is the set of all Archimedean valuations of 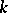 , then
, then
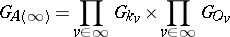 |
is known as the subgroup of integer adèles. If 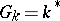 , then the number of different double cosets of the type
, then the number of different double cosets of the type 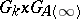 of the adèle group
of the adèle group 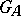 is finite and equal to the number of ideal classes of
is finite and equal to the number of ideal classes of 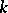 . The naturally arising problem as to whether the number of such double classes for an arbitrary algebraic group is finite is connected with the reduction theory for subgroups of principal adèles, i.e. with the construction of fundamental domains for the quotient space
. The naturally arising problem as to whether the number of such double classes for an arbitrary algebraic group is finite is connected with the reduction theory for subgroups of principal adèles, i.e. with the construction of fundamental domains for the quotient space 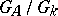 . It has been shown [5] that
. It has been shown [5] that 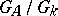 is compact if and only if the group
is compact if and only if the group 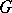 is
is 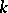 -anisotropic (cf. Anisotropic group). Another problem that has been solved are the circumstances under which the quotient space
-anisotropic (cf. Anisotropic group). Another problem that has been solved are the circumstances under which the quotient space 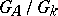 over an algebraic number field has finite volume in the Haar measure. Since
over an algebraic number field has finite volume in the Haar measure. Since 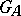 is locally compact, such a measure always exists, and the volume of
is locally compact, such a measure always exists, and the volume of 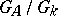 in the Haar measure is finite if and only if the group
in the Haar measure is finite if and only if the group 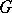 has no rational
has no rational  -characters (cf. Character of a group). The number
-characters (cf. Character of a group). The number 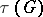 — the volume of
— the volume of 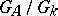 — is an important arithmetical invariant of the algebraic group G (cf. Tamagawa number). It was shown on the strength of these results [5] that the decomposition
— is an important arithmetical invariant of the algebraic group G (cf. Tamagawa number). It was shown on the strength of these results [5] that the decomposition
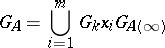 |
is valid for an arbitrary algebraic group 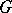 . If
. If 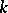 is a function field, it was also proved that the number of double classes of this kind for the adèle group of the algebraic group is finite, and an analogue of the reduction theory was developed [6]. For various arithmetical applications of adèle groups see [4], [7].
is a function field, it was also proved that the number of double classes of this kind for the adèle group of the algebraic group is finite, and an analogue of the reduction theory was developed [6]. For various arithmetical applications of adèle groups see [4], [7].
References
| [1] | A. Weil, "Adèles and algebraic groups" , Princeton Univ. Press (1961) |
| [2a] | T. Tamagawa, "Adéles" , Algebraic groups and discontinuous subgroups , Proc. Symp. Pure Math. , 9 , Amer. Math. Soc. (1966) pp. 113–121 |
| [2b] | M. Kneser, "Strong approximation" , Algebraic groups and discontinuous subgroups , Proc. Symp. Pure Math. , 9 , Amer. Math. Soc. (1966) pp. 187–198 |
| [3] | J.W.S. Cassels (ed.) A. Fröhlich (ed.) , Algebraic number theory , Acad. Press (1967) |
| [4] | V.P. Platonov, "Algebraic groups" J. Soviet Math. , 4 : 5 (1975) pp. 463–482 Itogi Nauk. Algebra Topol. Geom. , 11 (1973) pp. 5–37 |
| [5] | A. Borel, "Some finiteness properties of adèle groups over number fields" Publ. Math. IHES : 16 (1963) pp. 5–30 |
| [6] | G. Harder, "Minkowskische Reduktionstheorie über Funktionenkörpern" Invent. Math. , 7 (1969) pp. 33–54 |
| [7] | V.P. Platonov, "The arithmetic theory of linear algebraic groups and number theory" Trudy Mat. Inst. Steklov. , 132 (1973) pp. 162–168 (In Russian) |
| [8] | A. Weil, "Basic number theory" , Springer (1974) |
Comments
Let 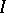 be an index set. For each
be an index set. For each 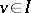 let
let 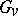 be a locally compact group and
be a locally compact group and 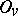 on open compact subgroup. The restricted (topological) direct product of the
on open compact subgroup. The restricted (topological) direct product of the 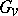 with respect to the
with respect to the 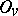 , above denoted by
, above denoted by
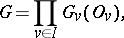 |
consists (as a set) of all 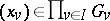 such that
such that 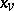 in
in  for all but finitely many
for all but finitely many  . The topology on
. The topology on 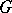 is defined by taking as a basis at the identity the open subgroups
is defined by taking as a basis at the identity the open subgroups 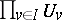 with
with 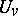 an open neighbourhood of
an open neighbourhood of 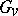 for all
for all  and
and 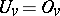 for all but finitely many
for all but finitely many  . This makes
. This makes  a locally compact topological group.
a locally compact topological group.
Adele group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Adele_group&oldid=14257