Additive selection

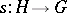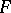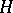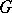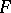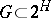A mapping associated with a set-valued function from an (Abelian) semi-group to subsets of an (Abelian) semi-group which is a homomorphism (of semi-groups) and a selection of . If and 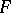is the identity transformation on 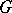, then is said to be an additive selection on 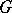. An archetypical example of an additive selection is the mapping which subordinates to each non-empty compact set in its maximal element. In 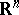, similar selections can be defined by means of lexicographic orders, see [a1] and Lexicographic order). They are Borel measurable but not continuous with respect to the Hausdorff metric (for 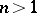). A Lipschitz-continuous additive selection on the family of convex bodies in 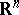is given by associating with each convex body its Steiner point, see [a2]. No such selections can exist in infinite dimensions, see [a3], [a4].

References

[a1]	R. Živaljević, "Extremal Minkowski additive selections of compact convex sets" Proc. Amer. Math. Soc. , 105 (1989) pp. 697–700
[a2]	R. Schneider, "Convex bodies: the Brunn–Minkowski theory" , Cambridge Univ. Press (1993)
[a3]	R.A. Vitale, "The Steiner point in infinite dimensions" Israel J. Math. , 52 (1985) pp. 245–250
[a4]	K. Przesławski, D. Yost, "Continuity properties of selectors and Michael's theorem" Michigan Math. J. , 36 (1989) pp. 113–134