ARK method
An  -stage adaptive Runge–Kutta method for the computation of approximations
-stage adaptive Runge–Kutta method for the computation of approximations  for the solution
for the solution  of an initial-value problem
of an initial-value problem
is given by
Here, 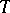 is an arbitrary matrix, for stability reasons usually
is an arbitrary matrix, for stability reasons usually 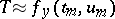 . For
. For 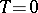 the method reduces to an explicit Runge–Kutta method. The
the method reduces to an explicit Runge–Kutta method. The 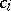 are real parameters and
are real parameters and 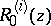 ,
, 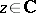 , are rational approximations to
, are rational approximations to 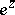 for
for 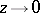 . The rational matrix functions
. The rational matrix functions  ,
, 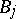 are defined by
are defined by
with 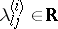 and
and
The computation of 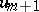 requires the solution of linear systems of algebraic equations only. The coefficients
requires the solution of linear systems of algebraic equations only. The coefficients 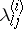 are determined to give a high order of consistency or B-consistency ([a2]). Applied to the test equation of A-stability,
are determined to give a high order of consistency or B-consistency ([a2]). Applied to the test equation of A-stability, 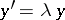 with
with 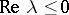 , an adaptive Runge–Kutta method with
, an adaptive Runge–Kutta method with 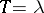 yields
yields
By the corresponding choice of stability functions 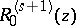 , adaptive Runge–Kutta methods are A- or L-stable and therefore well suited for stiff systems (cf. Stiff differential system). Furthermore, they can be easily adapted to the numerical solution of partitioned systems, where only a subsystem of dimension
, adaptive Runge–Kutta methods are A- or L-stable and therefore well suited for stiff systems (cf. Stiff differential system). Furthermore, they can be easily adapted to the numerical solution of partitioned systems, where only a subsystem of dimension 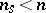 is stiff. Here, by a corresponding choice of
is stiff. Here, by a corresponding choice of 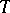 the dimension of the linear systems to be solved can be reduced to
the dimension of the linear systems to be solved can be reduced to 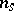 [a1].
[a1].
References
| [a1] | K. Strehmel, R. Weiner, "Partitioned adaptive Runge–Kutta methods and their stability" Numer. Math. , 45 (1984) pp. 283–300 |
| [a2] | K. Strehmel, R. Weiner, "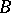 -convergence results for linearly implicit one step methods" BIT , 27 (1987) pp. 264–281 -convergence results for linearly implicit one step methods" BIT , 27 (1987) pp. 264–281 |
How to Cite This Entry:
Adaptive Runge–Kutta method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Adaptive_Runge%E2%80%93Kutta_method&oldid=15631
This article was adapted from an original article by R. Weiner (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article -stage adaptive Runge–Kutta method for the computation of approximations
-stage adaptive Runge–Kutta method for the computation of approximations  for the solution
for the solution  of an initial-value problem
of an initial-value problem
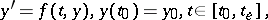
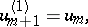
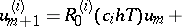
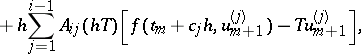
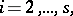
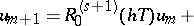
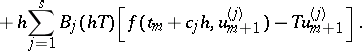
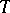 is an arbitrary matrix, for stability reasons usually
is an arbitrary matrix, for stability reasons usually 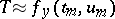 . For
. For 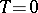 the method reduces to an explicit Runge–Kutta method. The
the method reduces to an explicit Runge–Kutta method. The 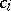 are real parameters and
are real parameters and 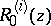 ,
, 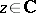 , are rational approximations to
, are rational approximations to 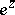 for
for 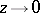 . The rational matrix functions
. The rational matrix functions  ,
, 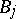 are defined by
are defined by
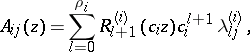
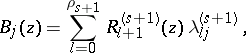
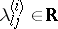 and
and

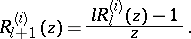
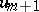 requires the solution of linear systems of algebraic equations only. The coefficients
requires the solution of linear systems of algebraic equations only. The coefficients 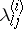 are determined to give a high order of consistency or B-consistency ([a2]). Applied to the test equation of A-stability,
are determined to give a high order of consistency or B-consistency ([a2]). Applied to the test equation of A-stability, 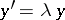 with
with 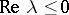 , an adaptive Runge–Kutta method with
, an adaptive Runge–Kutta method with 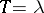 yields
yields
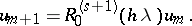
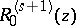 , adaptive Runge–Kutta methods are A- or L-stable and therefore well suited for stiff systems (cf. Stiff differential system). Furthermore, they can be easily adapted to the numerical solution of partitioned systems, where only a subsystem of dimension
, adaptive Runge–Kutta methods are A- or L-stable and therefore well suited for stiff systems (cf. Stiff differential system). Furthermore, they can be easily adapted to the numerical solution of partitioned systems, where only a subsystem of dimension 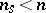 is stiff. Here, by a corresponding choice of
is stiff. Here, by a corresponding choice of 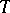 the dimension of the linear systems to be solved can be reduced to
the dimension of the linear systems to be solved can be reduced to 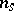 [a1].
[a1].
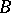 -convergence results for linearly implicit one step methods" BIT , 27 (1987) pp. 264–281
-convergence results for linearly implicit one step methods" BIT , 27 (1987) pp. 264–281