Adams–Hilton model
The Pontryagin algebra  (cf. also Pontryagin invariant; Pontryagin class) of a topological space
(cf. also Pontryagin invariant; Pontryagin class) of a topological space  is an important homotopy invariant (cf. also Homotopy type). It is, in general, quite difficult to calculate the homology
is an important homotopy invariant (cf. also Homotopy type). It is, in general, quite difficult to calculate the homology  directly from the chain complex
directly from the chain complex 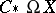 . An algorithm that associates to a space
. An algorithm that associates to a space  a differential graded algebra whose homology is relatively easy to calculate and isomorphic as an algebra to
a differential graded algebra whose homology is relatively easy to calculate and isomorphic as an algebra to 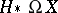 is therefore of great value.
is therefore of great value.
In 1955, J.F. Adams and P.J. Hilton invented such an algorithm for the class of simply-connected CW-complexes [a1]. Presented here in a somewhat more modern incarnation, due to S. Halperin, Y. Félix and J.-C. Thomas [a5], the work of Adams and Hilton can be summarized as follows.
Let  be a CW-complex such that
be a CW-complex such that  has exactly one
has exactly one  -cell and no
-cell and no 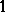 -cells and such that every attaching mapping is based with respect to the unique
-cells and such that every attaching mapping is based with respect to the unique  -cell of
-cell of  . There exists a morphism of differential graded algebras inducing an isomorphism on homology (a quasi-isomorphism)
. There exists a morphism of differential graded algebras inducing an isomorphism on homology (a quasi-isomorphism)
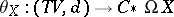 |
such that 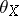 restricts to quasi-isomorphisms
restricts to quasi-isomorphisms  , where
, where 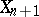 denotes the
denotes the 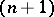 -skeleton of
-skeleton of 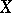 ,
, 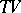 denotes the free (tensor) algebra on a free graded
denotes the free (tensor) algebra on a free graded  -module
-module 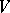 , and
, and 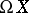 is the space of Moore loops on
is the space of Moore loops on 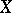 . The morphism
. The morphism 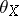 is called an Adams–Hilton model of
is called an Adams–Hilton model of 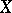 and satisfies the following properties.
and satisfies the following properties.
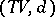 is unique up to isomorphism;
is unique up to isomorphism;
if 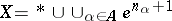 , then
, then 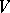 has a degree-homogeneous basis
has a degree-homogeneous basis 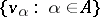 such that
such that 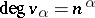 ;
;
if  is the attaching mapping of the cell
is the attaching mapping of the cell 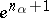 , then
, then 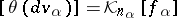 . Here,
. Here, 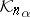 is defined so that
is defined so that
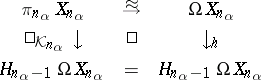 |
commutes, where 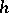 denotes the Hurewicz homomorphism (cf. Homotopy group).
denotes the Hurewicz homomorphism (cf. Homotopy group).
The Adams–Hilton model has proved to be a powerful tool for calculating the Pontryagin algebra of CW-complexes. Many common spaces have Adams–Hilton models that are relatively simple and thus well-adapted to computations. For example, with respect to its usual CW-decomposition, the Adams–Hilton model of  is
is 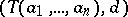 , where
, where 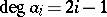 and
and 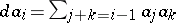 .
.
Given a cellular mapping  between CW-complexes, it is possible to use the Adams–Hilton model to compute the induced homomorphism of Pontryagin algebras. If
between CW-complexes, it is possible to use the Adams–Hilton model to compute the induced homomorphism of Pontryagin algebras. If  and
and 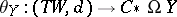 are Adams–Hilton models, then there exists a unique homotopy class of morphisms
are Adams–Hilton models, then there exists a unique homotopy class of morphisms 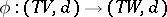 such that
such that 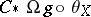 is homotopic to
is homotopic to 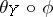 . Any representative
. Any representative 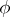 of this homotopy class can be said to be an Adams–Hilton model of
of this homotopy class can be said to be an Adams–Hilton model of  . In this context, "homotopy" means homotopy in the category of differential graded algebras (see [a2] or [a5] for more details).
. In this context, "homotopy" means homotopy in the category of differential graded algebras (see [a2] or [a5] for more details).
One can say, for example, that an Adams–Hilton model of a cellular co-fibration of CW-complexes, i.e., an inclusion of CW-complexes, is a free extension of differential graded algebras. Furthermore, the Adams–Hilton model of the amalgamated sum of an inclusion of CW-complexes,  , and any other cellular mapping
, and any other cellular mapping 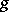 is given by the amalgamated sum of the free extension modelling
is given by the amalgamated sum of the free extension modelling  and an Adams–Hilton model of
and an Adams–Hilton model of 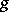 .
.
Examples of problems to which Adams–Hilton models have been applied to great advantage include the study of the holonomy action in fibrations [a4] and the study of the effect on the Pontryagin algebra of the attachment of a cell to a CW-complex [a3], [a6].
References
| [a1] | J.F. Adams, P.J. Hilton, "On the chain algebra of a loop space" Comment. Math. Helv. , 30 (1955) pp. 305–330 |
| [a2] | D.J. Anick, "Hopf algebras up to homotopy" J. Amer. Math. Soc. , 2 (1989) pp. 417–453 |
| [a3] | Y. Félix, J.-M. Lemaire, "On the Pontrjagin algebra of the loops on a space with a cell attached" Internat. J. Math. , 2 (1991) |
| [a4] | Y. Félix, J.-C. Thomas, "Module d'holonomie d'une fibration" Bull. Soc. Math. France , 113 (1985) pp. 255–258 |
| [a5] | S. Halperin, Y. Félix, J.-C. Thomas, "Rational homotopy theory" , Univ. Toronto (1996) (Preprint) |
| [a6] | K. Hess, J.-M- Lemaire, "Nice and lazy cell attachments" J. Pure Appl. Algebra , 112 (1996) pp. 29–39 |
Adams–Hilton model. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Adams%E2%80%93Hilton_model&oldid=13076