Difference between revisions of "Acyclic orientation"
(Importing text file) |
m (link) |
||
| Line 7: | Line 7: | ||
An edge in an acyclic orientation is dependent when reversing it would create a cycle. The acyclic orientation graph <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110280/a11028039.png" /> is the graph whose vertices are the acyclic orientations of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110280/a11028040.png" />, with two vertices adjacent when they differ by the reversal of an edge; the degree of a vertex is its number of independent edges. Every acyclic orientation of a connected <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110280/a11028041.png" />-vertex graph <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110280/a11028042.png" /> has at least <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110280/a11028043.png" /> independent edges (deletion of dependent edges does not disconnect <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110280/a11028044.png" />), and this is best possible (equality holds when the independent edges arise from a depth-first search tree). Thus, the minimum degree of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110280/a11028045.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110280/a11028046.png" />. P.H. Edelman (see also [[#References|[a10]]]) proved that the connectivity of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110280/a11028047.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110280/a11028048.png" />. | An edge in an acyclic orientation is dependent when reversing it would create a cycle. The acyclic orientation graph <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110280/a11028039.png" /> is the graph whose vertices are the acyclic orientations of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110280/a11028040.png" />, with two vertices adjacent when they differ by the reversal of an edge; the degree of a vertex is its number of independent edges. Every acyclic orientation of a connected <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110280/a11028041.png" />-vertex graph <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110280/a11028042.png" /> has at least <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110280/a11028043.png" /> independent edges (deletion of dependent edges does not disconnect <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110280/a11028044.png" />), and this is best possible (equality holds when the independent edges arise from a depth-first search tree). Thus, the minimum degree of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110280/a11028045.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110280/a11028046.png" />. P.H. Edelman (see also [[#References|[a10]]]) proved that the connectivity of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110280/a11028047.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110280/a11028048.png" />. | ||
| − | When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110280/a11028049.png" /> has <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110280/a11028050.png" /> edges, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110280/a11028051.png" /> is isomorphic to an induced subgraph of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110280/a11028053.png" />-dimensional hypercube and is thus bipartite (cf. [[Graph, bipartite|Graph, bipartite]]). It is conjectured that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110280/a11028054.png" /> is Hamiltonian when its two partite sets have the same size. G. Pruesse and F. Ruskey [[#References|[a8]]] proved that the Cartesian product <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110280/a11028055.png" /> is always Hamiltonian. These Hamiltonicity questions relate to the combinatorial Gray code problem (cf. [[Gray code|Gray code]]) of listing the acyclic orientations by reversing one edge at a time. | + | When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110280/a11028049.png" /> has <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110280/a11028050.png" /> edges, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110280/a11028051.png" /> is isomorphic to an [[induced subgraph]] of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110280/a11028053.png" />-dimensional hypercube and is thus bipartite (cf. [[Graph, bipartite|Graph, bipartite]]). It is conjectured that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110280/a11028054.png" /> is Hamiltonian when its two partite sets have the same size. G. Pruesse and F. Ruskey [[#References|[a8]]] proved that the Cartesian product <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110280/a11028055.png" /> is always Hamiltonian. These Hamiltonicity questions relate to the combinatorial Gray code problem (cf. [[Gray code|Gray code]]) of listing the acyclic orientations by reversing one edge at a time. |
When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110280/a11028056.png" /> is less than the girth of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110280/a11028057.png" />, the list of vertex degrees in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110280/a11028058.png" /> includes all values from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110280/a11028059.png" /> up to the maximum degree [[#References|[a4]]]. It is unknown whether this is true for all graphs. When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110280/a11028060.png" />, there exist acyclic orientations in which every edge is independent. | When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110280/a11028056.png" /> is less than the girth of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110280/a11028057.png" />, the list of vertex degrees in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110280/a11028058.png" /> includes all values from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110280/a11028059.png" /> up to the maximum degree [[#References|[a4]]]. It is unknown whether this is true for all graphs. When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110280/a11028060.png" />, there exist acyclic orientations in which every edge is independent. | ||
Revision as of 14:45, 10 January 2016
An orientation (assignment of direction) of each edge of a graph such that no cycle in the graph is a cycle (consistently oriented) in the resulting directed graph (cf. Graph, oriented).
An acyclic orientation of a graph  can be obtained from a proper colouring
can be obtained from a proper colouring  by orienting each edge
by orienting each edge 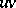 from
from  to
to  if
if  (cf. Graph colouring). Given an acyclic orientation
(cf. Graph colouring). Given an acyclic orientation  of a connected graph
of a connected graph  that is not a forest (cf. also Graph, connectivity of a), let
that is not a forest (cf. also Graph, connectivity of a), let  be the maximum over all cycles in
be the maximum over all cycles in 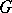 of
of 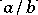 , where
, where 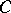 has
has  forward edges and
forward edges and  backward edges in
backward edges in  . G.J. Minty [a7] proved that
. G.J. Minty [a7] proved that 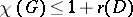 and that this is best possible (equality holds for the acyclic orientation obtained above from an optimal colouring). Minty's theorem implies the related Gallai–Roy theorem ([a5], [a9], [a14]) that
and that this is best possible (equality holds for the acyclic orientation obtained above from an optimal colouring). Minty's theorem implies the related Gallai–Roy theorem ([a5], [a9], [a14]) that 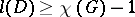 where
where 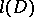 is the maximum length of a path in an orientation
is the maximum length of a path in an orientation  of
of  (equality holds for the orientation defined above).
(equality holds for the orientation defined above).
R.P. Stanley [a11] proved that the number of acyclic orientations of a graph  is the value at
is the value at 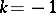 of the chromatic polynomial
of the chromatic polynomial 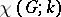 (computing this number is
(computing this number is  -complete [a13]). More generally, suppose that
-complete [a13]). More generally, suppose that 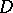 is an acyclic orientation of an
is an acyclic orientation of an  -vertex graph
-vertex graph  and that
and that  is a
is a  -colouring of
-colouring of  . One says that
. One says that 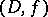 is a compatible pair if
is a compatible pair if 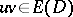 implies
implies 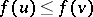 . Stanley proved that the number of compatible pairs is
. Stanley proved that the number of compatible pairs is 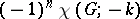 . This relationship is an instance of combinatorial reciprocity. Stanley [a12] further generalized this to count acyclic orientations with
. This relationship is an instance of combinatorial reciprocity. Stanley [a12] further generalized this to count acyclic orientations with 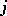 sinks. C. Greene [a6] proved that the acyclic orientations of a graph
sinks. C. Greene [a6] proved that the acyclic orientations of a graph 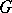 are in one-to-one correspondence with the regions of an associated arrangement of hyperplanes; T. Zaslavsky [a15] has generalized this to acyclic orientations of signed graphs.
are in one-to-one correspondence with the regions of an associated arrangement of hyperplanes; T. Zaslavsky [a15] has generalized this to acyclic orientations of signed graphs.
An edge in an acyclic orientation is dependent when reversing it would create a cycle. The acyclic orientation graph  is the graph whose vertices are the acyclic orientations of
is the graph whose vertices are the acyclic orientations of  , with two vertices adjacent when they differ by the reversal of an edge; the degree of a vertex is its number of independent edges. Every acyclic orientation of a connected
, with two vertices adjacent when they differ by the reversal of an edge; the degree of a vertex is its number of independent edges. Every acyclic orientation of a connected  -vertex graph
-vertex graph 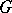 has at least
has at least 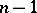 independent edges (deletion of dependent edges does not disconnect
independent edges (deletion of dependent edges does not disconnect  ), and this is best possible (equality holds when the independent edges arise from a depth-first search tree). Thus, the minimum degree of
), and this is best possible (equality holds when the independent edges arise from a depth-first search tree). Thus, the minimum degree of  is
is  . P.H. Edelman (see also [a10]) proved that the connectivity of
. P.H. Edelman (see also [a10]) proved that the connectivity of 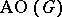 is
is  .
.
When  has
has 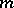 edges,
edges, 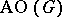 is isomorphic to an induced subgraph of the
is isomorphic to an induced subgraph of the  -dimensional hypercube and is thus bipartite (cf. Graph, bipartite). It is conjectured that
-dimensional hypercube and is thus bipartite (cf. Graph, bipartite). It is conjectured that 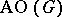 is Hamiltonian when its two partite sets have the same size. G. Pruesse and F. Ruskey [a8] proved that the Cartesian product
is Hamiltonian when its two partite sets have the same size. G. Pruesse and F. Ruskey [a8] proved that the Cartesian product 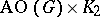 is always Hamiltonian. These Hamiltonicity questions relate to the combinatorial Gray code problem (cf. Gray code) of listing the acyclic orientations by reversing one edge at a time.
is always Hamiltonian. These Hamiltonicity questions relate to the combinatorial Gray code problem (cf. Gray code) of listing the acyclic orientations by reversing one edge at a time.
When 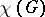 is less than the girth of
is less than the girth of  , the list of vertex degrees in
, the list of vertex degrees in 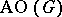 includes all values from
includes all values from  up to the maximum degree [a4]. It is unknown whether this is true for all graphs. When
up to the maximum degree [a4]. It is unknown whether this is true for all graphs. When  , there exist acyclic orientations in which every edge is independent.
, there exist acyclic orientations in which every edge is independent.
A graph has an acyclic orientation in which every edge is independent if and only if it is a cover graph; this acyclic orientation is the cover relation of a partially ordered set (cf. Partial order). Recognition of cover graphs is 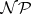 -complete. The smallest triangle-free graph with chromatic number
-complete. The smallest triangle-free graph with chromatic number 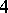 (violating the condition
(violating the condition 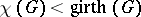 ) is the
) is the 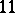 -vertex Grötzsch graph, and it is not a cover graph.
-vertex Grötzsch graph, and it is not a cover graph.
Other types of acyclic orientations characterize important families of graphs. An acyclic orientation 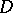 of a simple graph is a transitive orientation if
of a simple graph is a transitive orientation if 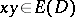 and
and 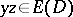 together imply
together imply 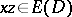 . The graphs having transitive orientations are the comparability graphs of partially ordered sets. A graph is perfectly orderable if it has a vertex ordering
. The graphs having transitive orientations are the comparability graphs of partially ordered sets. A graph is perfectly orderable if it has a vertex ordering  such that greedily colouring the vertices of any induced subgraph
such that greedily colouring the vertices of any induced subgraph  in the order specified by
in the order specified by  uses only
uses only 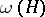 colours, where
colours, where 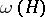 is the size of the largest clique in
is the size of the largest clique in  . V. Chvátal [a3] proved that
. V. Chvátal [a3] proved that  is perfectly orderable if and only if it has an acyclic orientation having no induced
is perfectly orderable if and only if it has an acyclic orientation having no induced  -vertex path with both end-edges oriented outward.
-vertex path with both end-edges oriented outward.
Let 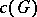 be the worst-case number of edges that must be probed by an algorithm that finds an unknown acyclic orientation of
be the worst-case number of edges that must be probed by an algorithm that finds an unknown acyclic orientation of  . A graph is exhaustive if
. A graph is exhaustive if 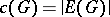 . Graphs having an acyclic orientation in which every edge is independent are exhaustive. For bounds on
. Graphs having an acyclic orientation in which every edge is independent are exhaustive. For bounds on  in terms of the independence number of
in terms of the independence number of  see [a1]. N. Alon and Zs. Tuza [a2] proved that for the random graph with constant edge probability
see [a1]. N. Alon and Zs. Tuza [a2] proved that for the random graph with constant edge probability  , almost surely
, almost surely 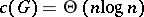 . Both papers also study exhaustive graphs.
. Both papers also study exhaustive graphs.
Acyclic orientations have computational applications in percolation, network reliability, neural networks, parallel sorting, scheduling, etc.
References
| [a1] | M. Aigner, E. Triesch, Zs. Tuza, "Searching for acyclic orientations of graphs" Discrete Math. , 144 (1995) pp. 3–10 (Combinatorics of Ordered Sets (Oberwolfach, 1991)) |
| [a2] | N. Alon, Zs. Tuza, "The acyclic orientation game on random graphs" Random Structures Algorithms , 6 (1995) pp. 261–268 (Proc. Sixth Internat. Sem. Random Graphs and Probabilistic Methods in Combinatorics and Computer Science, (Random Graphs '93; Poznań, 1993)) |
| [a3] | V. Chvátal, "Perfectly ordered graphs" , Topics on perfect graphs , North-Holland math. stud. , 88 , North-Holland (1984) pp. 63–65 |
| [a4] | D.C. Fisher, K. Fraughnaugh, L. Langley, D.B. West, "The number of dependent edges in an acyclic orientation" J. Combin. Th. Appl. (to appear) |
| [a5] | T. Gallai, "On directed paths and circuits" P. Erdős (ed.) G. Katona (ed.) , Theory of Graphs (Proc. Tihany 1966) , Acad. Press (1968) pp. 115–118 |
| [a6] | C. Greene, "Acyclic orientations" M. Aigner (ed.) , Higher combinatorics , Proc. NATO Adv. Study Inst. (1976) , Reidel (1977) pp. 65–68 |
| [a7] | G.J. Minty, "A theorem on  -coloring the points of a linear graph" Amer. Math. Monthly , 69 (1962) pp. 623–624 -coloring the points of a linear graph" Amer. Math. Monthly , 69 (1962) pp. 623–624 |
| [a8] | G. Pruesse, F. Ruskey, "The prism of the acyclic orientation graph is Hamiltonian" Electron. J. Combin. , 2 (1995) (Research Paper 5, approx. 6 pp. (electronic)) |
| [a9] | B. Roy, "Nombre chromatique et plus longs chemins d'un graphe" Rev. Française Automat. Informat. Recherche Opérationelle Ser. Rouge , 1 (1967) pp. 127–132 |
| [a10] | C.D. Savage, C.-Q. Zhang, "A note on the connectivity of acyclic orientation graphs" Discrete Math. (to appear) |
| [a11] | R.P. Stanley, "Acyclic orientations of graphs" Discrete Math. , 5 (1973) pp. 171–178 |
| [a12] | R.P. Stanley, "A symmetric function generalization of the chromatic polynomial of a graph" Adv. Math. , 111 (1995) pp. 166–194 |
| [a13] | D.L. Vertigan, D.J.A. Welsh, "The computational complexity of the Tutte plane: the bipartite case" Combin. Probab. Comput. , 1 (1992) pp. 181–187 |
| [a14] | L.M. Vitaver, "Determination of minimal coloring of vertices of a graph by means of Boolean powers of the incidence matrix" Dokl. Akad. Nauk. SSSR , 147 (1962) pp. 758–759 (In Russian) |
| [a15] | T. Zaslavsky, "Orientation of signed graphs" European J. Combin. , 12 (1991) pp. 361–375 |
Acyclic orientation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Acyclic_orientation&oldid=11691