Acceleration wave
In the mechanics of continuous media, the behaviour of a material body is described by a number of field variables which are required to satisfy a set of governing partial differential equations arising from balance laws, and from kinematic and constitutive considerations. The variables are generally assumed to have the requisite degree of smoothness consistent with the governing equations, except possibly on surfaces in the body across which some of the variables may suffer jump discontinuities (cf. also Smooth function).
Suppose that a material body occupies a region  in
in 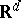 at time
at time 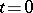 , and at some later time
, and at some later time 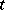 occupies, in its deformed state, a region
occupies, in its deformed state, a region 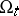 . The motion of the body is described by the function
. The motion of the body is described by the function 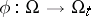 ,
, 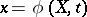 , in which
, in which 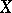 denotes the position at time
denotes the position at time 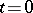 of a material particle, and
of a material particle, and  its position at time
its position at time 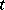 . The function
. The function 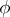 is assumed to be invertible, and both
is assumed to be invertible, and both 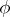 and its inverse are assumed to be continuously differentiable with respect to the spatial and temporal variables on which they depend, except possibly on specified surfaces in the body. A propagating smooth surface divides the body
and its inverse are assumed to be continuously differentiable with respect to the spatial and temporal variables on which they depend, except possibly on specified surfaces in the body. A propagating smooth surface divides the body 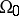 or
or 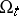 into two regions, forming a common boundary between them. The unit normal
into two regions, forming a common boundary between them. The unit normal  to the surface
to the surface 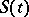 is considered to be in the direction in which
is considered to be in the direction in which 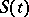 propagates. The region ahead of the surface is denoted by
propagates. The region ahead of the surface is denoted by 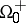 and the region behind the surface is denoted by
and the region behind the surface is denoted by 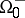 . Let
. Let 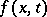 be an arbitrary scalar-, vector- or tensor-valued function which is continuous in both
be an arbitrary scalar-, vector- or tensor-valued function which is continuous in both 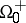 and
and 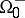 . This function has definite limits
. This function has definite limits 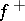 and
and  at a point on
at a point on 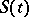 , as the point is approached from
, as the point is approached from 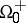 and
and 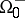 . The jump of
. The jump of 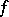 at
at 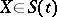 is defined by
is defined by
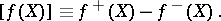 | (a1) |
The surface 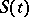 is called a singular surface with respect to
is called a singular surface with respect to 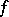 at time
at time 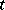 if
if 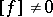 . A singular surface that has a non-zero normal velocity called a wave. An acceleration wave is a propagating singular surface across which the motion
. A singular surface that has a non-zero normal velocity called a wave. An acceleration wave is a propagating singular surface across which the motion 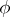 , velocity
, velocity 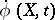 and (hence) the deformation gradient
and (hence) the deformation gradient 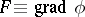 , are continuous; however, quantities involving second-order derivatives of the motion, such as the acceleration
, are continuous; however, quantities involving second-order derivatives of the motion, such as the acceleration  and the time rate of deformation gradient
and the time rate of deformation gradient 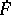 , are discontinuous. Various kinematical and geometrical conditions of compatibility involving the variables
, are discontinuous. Various kinematical and geometrical conditions of compatibility involving the variables  and
and 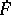 , the normal
, the normal  to the surface, and the speed
to the surface, and the speed 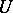 of the surface, may be derived with the aid of Hadamard's lemma (see, for example, [a2], [a4]). These considerations lead to the propagation condition
of the surface, may be derived with the aid of Hadamard's lemma (see, for example, [a2], [a4]). These considerations lead to the propagation condition
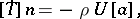 | (a2) |
which is a statement of balance of linear momentum across the surface; 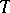 is the Cauchy stress,
is the Cauchy stress, 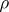 is the mass density, and
is the mass density, and 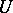 is the intrinsic speed of the surface. To make further progress it is necessary to introduce information about the constitution of the material; in the case of an elastic material, for example, (a2) becomes the eigenvalue problem
is the intrinsic speed of the surface. To make further progress it is necessary to introduce information about the constitution of the material; in the case of an elastic material, for example, (a2) becomes the eigenvalue problem
 | (a3) |
in which  is referred to as the amplitude vector of the acceleration jump, and
is referred to as the amplitude vector of the acceleration jump, and 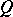 is the acoustic tensor. This leads to the Fresnel–Hadamard theorem: The amplitude
is the acoustic tensor. This leads to the Fresnel–Hadamard theorem: The amplitude  of an acceleration wave travelling in the direction
of an acceleration wave travelling in the direction  must be an eigenvector of the acoustic tensor
must be an eigenvector of the acoustic tensor 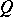 ; the corresponding eigenvalue is
; the corresponding eigenvalue is 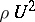 . It follows that, for real wave speeds to exist,
. It follows that, for real wave speeds to exist, 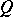 must possess at least one real and positive eigenvalue. The acoustic tensor is symmetric, and consequently its eigenvalues are real, if and only if the material is hyperelastic. In addition,
must possess at least one real and positive eigenvalue. The acoustic tensor is symmetric, and consequently its eigenvalues are real, if and only if the material is hyperelastic. In addition, 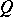 possesses three positive eigenvalues if and only if it is positive definite; in the context of elasticity, positive definiteness of
possesses three positive eigenvalues if and only if it is positive definite; in the context of elasticity, positive definiteness of 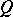 implies that the material is strongly elliptic. Further information on acceleration waves may be found in the references cited.
implies that the material is strongly elliptic. Further information on acceleration waves may be found in the references cited.
References
| [a1] | A.C. Eringen, E.S. Suhubi, "Elastodynamics" , I , Acad. Press (1975) |
| [a2] | J. Hadamard, "Leçons sur la propagation des ondes et les équations de l'hydrodynamique" , Dunod (1903) |
| [a3] | M.F. McCarthy, "Singular surfaces and waves" A.C. Eringen (ed.) , Continuum Physics II: Continuum Mechanics of Single Surface Bodies , Acad. Press (1975) |
| [a4] | C.-C. Wang, C. Truesdell, "Introduction to rational elasticity" , Noordhoff (1973) |
Acceleration wave. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Acceleration_wave&oldid=12663