Abstract hyperbolic differential equation
Consider the Cauchy problem for the symmetric hyperbolic system (cf. also Hyperbolic partial differential equation)
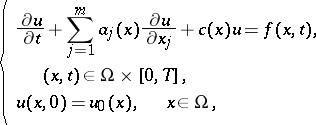 |
with the boundary conditions
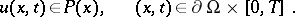 |
Here, 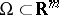 is a bounded domain with smooth boundary
is a bounded domain with smooth boundary  (when
(when  , no boundary conditions are necessary), and
, no boundary conditions are necessary), and  ,
, 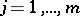 , and
, and  are smooth functions on
are smooth functions on  with as values real matrices in
with as values real matrices in 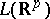 , the
, the  being symmetric. It is assumed that the boundary matrix
being symmetric. It is assumed that the boundary matrix 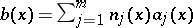 ,
, 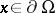 , is non-singular, where
, is non-singular, where 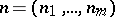 is the unit outward normal vector to
is the unit outward normal vector to  . Also,
. Also, 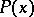 denotes the maximal non-negative subspace of
denotes the maximal non-negative subspace of  with respect to
with respect to 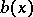 , i.e.
, i.e. 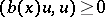 ,
, 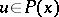 , and
, and  is not a proper subset of any other subspace of
is not a proper subset of any other subspace of 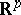 with this property. The function
with this property. The function 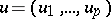 is the unknown function.
is the unknown function.
One can handle this problem as the Cauchy problem for an evolution equation in a Banach space (cf. also Linear differential equation in a Banach space). Indeed, let  be the smallest closed extension in
be the smallest closed extension in 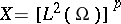 of the operator
of the operator  defined by
defined by
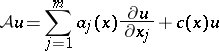 |
with domain
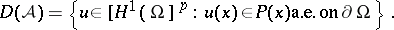 |
Then  is the negative generator of a
is the negative generator of a  semi-group on
semi-group on  (cf. [a1], [a2]; see also Semi-group of operators). Hence, the Hille–Yoshida theorem proves the existence of a unique solution
(cf. [a1], [a2]; see also Semi-group of operators). Hence, the Hille–Yoshida theorem proves the existence of a unique solution 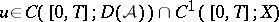 to the Cauchy problem
to the Cauchy problem
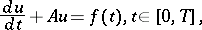 |
which is given in the form
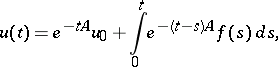 |
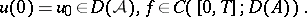 |
Next to this idea of an abstract formulation for hyperbolic systems, the study of the linear evolution equation
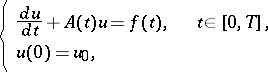 |
was originated by T. Kato, and was developed by him and many others (cf. [a3], Chap. 7). Here, 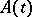 denotes a given function with values in the space of closed linear operators acting in a Banach space
denotes a given function with values in the space of closed linear operators acting in a Banach space  ;
; 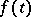 and
and 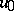 are the initial data, and
are the initial data, and 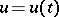 is the unknown function with values in
is the unknown function with values in 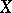 .
.
Among others, Kato's theorem in [a4] is fundamental: Suppose that
I) 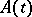 is a stable family on
is a stable family on 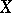 , in the sense that
, in the sense that
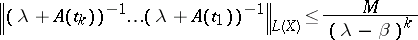 |
for any 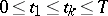 and any
and any  with some fixed
with some fixed 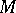 and
and  .
.
II) There is a second Banach space, 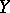 , such that
, such that  , and
, and 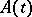 is a continuous function of
is a continuous function of  with values in
with values in 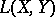 .
.
III) There is an isomorphism 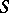 from
from  onto
onto  such that
such that 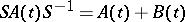 , with
, with 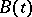 a strongly continuous function of
a strongly continuous function of  with values in
with values in 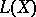 . Then there is a unique solution
. Then there is a unique solution 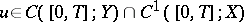 , and it is given by
, and it is given by
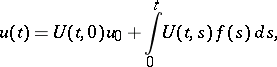 |
 ,
, 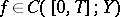 , where
, where  is a unique evolution operator. It is easily seen that III) implies, in particular, the stability of
is a unique evolution operator. It is easily seen that III) implies, in particular, the stability of 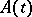 on
on  . When
. When  and
and 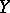 are Hilbert spaces, III) can be replaced by the simpler condition [a5]:
are Hilbert spaces, III) can be replaced by the simpler condition [a5]:
III') There exists a positive-definite self-adjoint operator  on
on 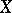 with
with  such that
such that 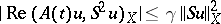 for any
for any 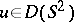 , with some constants
, with some constants 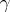 .
.
The Cauchy problem for the quasi-linear differential equation
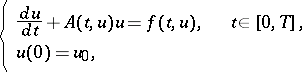 |
has been studied by several mathematicians on the basis of results for linear problems, [a7]. Here, 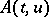 depends also on the unknown function
depends also on the unknown function  . In [a6], [a7],
. In [a6], [a7], 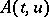 , defined for
, defined for 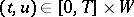 , where
, where 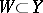 is a bounded open set, is assumed to satisfy conditions similar to I)–III) and a Lipschitz condition
is a bounded open set, is assumed to satisfy conditions similar to I)–III) and a Lipschitz condition 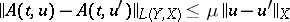 with respect to
with respect to  . Under such conditions, the existence and uniqueness of a local solution, continuous dependence on the initial data and applications to quasi-linear hyperbolic systems have been given.
. Under such conditions, the existence and uniqueness of a local solution, continuous dependence on the initial data and applications to quasi-linear hyperbolic systems have been given.
References
| [a1] | E. Hille, R.S. Phillips, "Functional analysis and semi-groups" , Amer. Math. Soc. (1957) |
| [a2] | K. Yoshida, "Functional analysis" , Springer (1957) |
| [a3] | H. Tanabe, "Functional analytic methods for partial differential equations" , M. Dekker (1997) |
| [a4] | T. Kato, "Linear evolution equations of "hyperbolic" type" J. Fac. Sci. Univ. Tokyo , 17 (1970) pp. 241–248 |
| [a5] | N. Okazawa, "Remarks on linear evolution equations of hyperbolic type in Hilbert space" Adv. Math. Sci. Appl. , 8 (1998) pp. 399–423 |
| [a6] | K. Kobayashi, N. Sanekata, "A method of iterations for quasi-linear evolution equations in nonreflexive Banach spaces" Hiroshima Math. J. , 19 (1989) pp. 521–540 |
| [a7] | T. Kato, "Abstract evolution equations, linear and quasilinear, revisited" J. Komatsu (ed.) , Funct. Anal. and Rel. Topics. Proc. Conf. in Memory of K. Yoshida (RIMS, 1991) , Lecture Notes Math. , 1540 , Springer (1991) pp. 103–125 |
Abstract hyperbolic differential equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Abstract_hyperbolic_differential_equation&oldid=15200