Abstract analytic function
analytic mapping of Banach spaces
A function  acting from some domain
acting from some domain 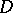 of a Banach space
of a Banach space 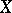 into a Banach space
into a Banach space 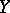 that is differentiable according to Fréchet everywhere in
that is differentiable according to Fréchet everywhere in 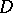 , i.e. is such that for any point
, i.e. is such that for any point 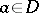 there exists a bounded linear operator
there exists a bounded linear operator 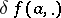 from
from 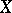 into
into 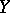 for which the following relation is true:
for which the following relation is true:
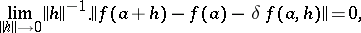 |
where 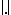 denotes the norm on
denotes the norm on  or on
or on 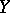 ;
; 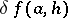 is called the Fréchet differential of
is called the Fréchet differential of 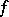 at
at  .
.
Another approach to the notion of an abstract analytic function is based on differentiability according to Gâteaux. A function 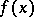 from
from 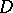 into
into 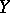 is weakly analytic in
is weakly analytic in 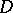 , or differentiable according to Gâteaux in
, or differentiable according to Gâteaux in 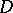 , if for each continuous linear functional
, if for each continuous linear functional 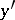 on
on 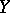 and each element
and each element 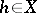 the complex function
the complex function 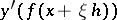 is a holomorphic function of the complex variable
is a holomorphic function of the complex variable 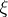 in the disc
in the disc 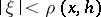 , where
, where  . Any abstract analytic function in a domain
. Any abstract analytic function in a domain 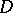 is continuous and weakly analytic in
is continuous and weakly analytic in 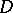 . The converse proposition is also true, and the continuity condition can be replaced by local boundedness or by continuity according to Baire.
. The converse proposition is also true, and the continuity condition can be replaced by local boundedness or by continuity according to Baire.
The term "abstract analytic function" is sometimes employed in a narrower sense, when it means a function 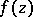 of a complex variable
of a complex variable  with values in a Banach space or even in a locally convex linear topological space
with values in a Banach space or even in a locally convex linear topological space 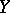 . In such a case any weakly analytic function
. In such a case any weakly analytic function 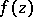 in a domain
in a domain 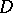 of the complex plane
of the complex plane 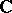 is an abstract analytic function. One can also say that a function
is an abstract analytic function. One can also say that a function 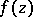 is an abstract analytic function in a domain
is an abstract analytic function in a domain 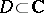 if and only if
if and only if 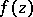 is continuous in
is continuous in 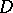 and if for any simple closed rectifiable contour
and if for any simple closed rectifiable contour 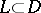 the integral
the integral  vanishes. For an abstract analytic function
vanishes. For an abstract analytic function 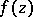 of a complex variable
of a complex variable  the Cauchy formula (cf. Cauchy integral) is valid.
the Cauchy formula (cf. Cauchy integral) is valid.
Let 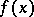 be a weakly analytic function in a domain
be a weakly analytic function in a domain 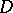 of a Banach space
of a Banach space  . Then
. Then 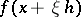 , as a function of the complex variable
, as a function of the complex variable 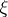 , has derivatives of all orders in the domain
, has derivatives of all orders in the domain 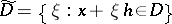 ,
, 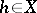 , these derivatives being abstract analytic functions from
, these derivatives being abstract analytic functions from 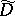 into
into 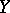 . If the set
. If the set 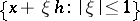 belongs to
belongs to 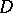 , then
, then
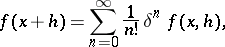 |
where the series converges in norm, and
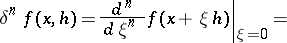 |
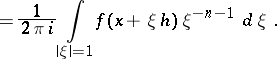 |
A function 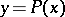 from
from 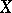 into
into 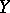 is called a polynomial with respect to the variable
is called a polynomial with respect to the variable  of degree at most
of degree at most 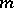 if, for all
if, for all 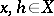 and for all complex
and for all complex 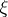 , one has
, one has
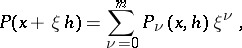 |
where the functions 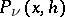 are independent of
are independent of 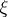 . The degree of
. The degree of 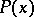 is exactly
is exactly 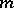 if
if 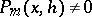 . A power series is a series of the form
. A power series is a series of the form 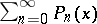 where
where 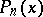 are homogeneous polynomials of degree
are homogeneous polynomials of degree  so that
so that 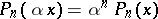 ,
, 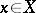 , for all complex
, for all complex 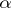 . An arbitrary weakly convergent power series
. An arbitrary weakly convergent power series  in a domain
in a domain 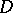 converges in norm towards some weakly analytic function
converges in norm towards some weakly analytic function 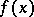 in
in 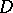 , and
, and 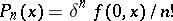 ,
, 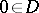 . A function
. A function 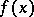 is an abstract analytic function if and only if it can be developed in a power series in a neighbourhood of all points
is an abstract analytic function if and only if it can be developed in a power series in a neighbourhood of all points 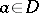
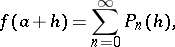 |
where all 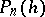 are continuous in
are continuous in 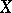 .
.
Many fundamental results in the classical theory of analytic functions — such as the maximum-modulus principle, the uniqueness theorems, the Vitali theorem, the Liouville theorem, etc. — are applicable to abstract analytic functions if suitable changes are introduced. The set of all analytic functions in a domain 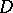 forms a linear space.
forms a linear space.
The notion of an abstract analytic function can be generalized to wider classes of spaces 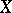 and
and 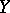 , such as locally convex topological spaces, Banach spaces over an arbitrary complete valuation field, etc.
, such as locally convex topological spaces, Banach spaces over an arbitrary complete valuation field, etc.
References
| [1] | E. Hille, R.S. Phillips, "Functional analysis and semi-groups" , Amer. Math. Soc. (1957) |
| [2] | R.E. Edwards, "Functional analysis: theory and applications" , Holt, Rinehart & Winston (1965) |
| [3] | L. Schwartz, "Cours d'analyse" , 2 , Hermann (1967) |
Abstract analytic function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Abstract_analytic_function&oldid=17260