Absolutely integrable function
A function such that its absolute value is integrable. If a function is Riemann-integrable on the segment 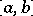 ,
, 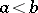 , its absolute value is also Riemann-integrable on this interval, and
, its absolute value is also Riemann-integrable on this interval, and
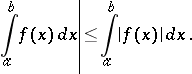 |
A similar assertion is also valid for a function of  variables which is Riemann-integrable on a cube-filled domain in the
variables which is Riemann-integrable on a cube-filled domain in the  -dimensional Euclidean space. The converse theorem for Riemann-integrable functions is not true: The function
-dimensional Euclidean space. The converse theorem for Riemann-integrable functions is not true: The function 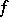 which is equal to 1 for rational values of
which is equal to 1 for rational values of  and is equal to
and is equal to 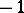 for irrational values of
for irrational values of  is not Riemann-integrable, but its absolute value is integrable. The situation is different for Lebesgue-integrable functions: A Lebesgue-measurable function
is not Riemann-integrable, but its absolute value is integrable. The situation is different for Lebesgue-integrable functions: A Lebesgue-measurable function 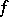 is Lebesgue-integrable (Lebesgue-summable) on a measurable set
is Lebesgue-integrable (Lebesgue-summable) on a measurable set 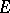 in the
in the  -dimensional space if and only if its absolute value is Lebesgue-integrable on this set. The following inequality is valid:
-dimensional space if and only if its absolute value is Lebesgue-integrable on this set. The following inequality is valid:
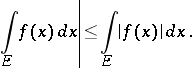 |
In the case of improper one-dimensional Riemann or Lebesgue integrals on a half-open interval 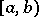 ,
, 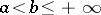 (provided that the function
(provided that the function 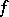 is, respectively, Riemann-integrable or Lebesgue-integrable on any segment
is, respectively, Riemann-integrable or Lebesgue-integrable on any segment 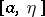 ,
, 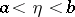 ), the existence of the improper integral of the absolute value of the function,
), the existence of the improper integral of the absolute value of the function,
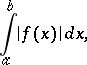 |
implies the existence of the integral
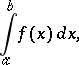 |
but the converse statement is not true (cf. Absolutely convergent improper integral). In this connection it should be noted that, if the improper integral
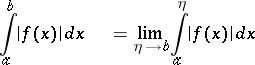 |
exists, then 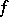 is Lebesgue-integrable on
is Lebesgue-integrable on  , and its improper integral is equal to the Lebesgue integral.
, and its improper integral is equal to the Lebesgue integral.
In the case of functions of several (more than one) variables, improper integrals are usually so defined that the existence of the improper integral of the absolute value of a function is equivalent to the existence of the improper integral of the function itself.
Let the values of a function 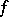 be in some Banach space with norm
be in some Banach space with norm 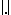 . The function
. The function  is then called absolutely integrable on a measurable set
is then called absolutely integrable on a measurable set 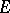 if the integral
if the integral
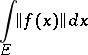 |
exists; also, if 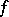 is integrable on
is integrable on 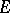 , the relationship
, the relationship
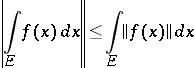 |
is true.
References
| [1] | V.A. Il'in, E.G. Poznyak, "Fundamentals of mathematical analysis" , 1–2 , MIR (1982) (Translated from Russian) |
| [2] | L.D. Kudryavtsev, "Mathematical analysis" , 1 , Moscow (1973) (In Russian) |
| [3] | S.M. Nikol'skii, "A course of mathematical analysis" , 1 , MIR (1977) (Translated from Russian) |
| [4] | L. Schwartz, "Cours d'analyse" , 1 , Hermann (1967) |
Comments
References
| [a1] | H.L. Royden, "Real analysis" , Macmillan (1968) |
| [a2] | A.C. Zaanen, "Integration" , North-Holland (1967) |
| [a3] | W. Rudin, "Principles of mathematical analysis" , McGraw-Hill (1953) |
| [a4] | W. Rudin, "Real and complex analysis" , McGraw-Hill (1966) pp. 98 |
| [a5] | A.E. Taylor, "General theory of functions and integration" , Blaisdell (1965) |
| [a6] | C.D. Aliprantz, O. Burleinshaw, "Principles of real analysis" , North-Holland (1981) |
Absolutely integrable function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Absolutely_integrable_function&oldid=16778