Absolute summability
A special type of summability of series and sequences, which differs from ordinary summability in that additional restrictions are imposed. For matrix summation methods the requirement is that the series and sequences obtained as a result of the transformation corresponding to the given summation method must be absolutely convergent (cf. Matrix summation method). Let a summation method 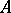 be defined as a transformation of sequences
be defined as a transformation of sequences 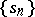 into sequences
into sequences 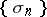 by means of the matrix
by means of the matrix 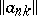 :
:
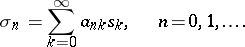 |
The sequence 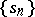 is then absolutely summable by the method
is then absolutely summable by the method 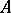 (
(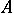 -summable) to the limit
-summable) to the limit  if it is
if it is 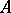 -summable to this limit, i.e. if
-summable to this limit, i.e. if
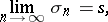 |
and if the sequence  is of bounded variation:
is of bounded variation:
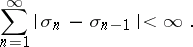 | (1) |
If the 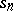 are the partial sums of a series
are the partial sums of a series
 | (2) |
then the series (2) is absolutely summable by the method 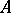 to the sum
to the sum  . Condition (1) is an additional requirement which makes absolute summability different from ordinary summability. Absolute summability is defined in a similar manner for methods involving matrix transformations of series into sequences. If the summation method is defined by a transformation of the series (2) into a series
. Condition (1) is an additional requirement which makes absolute summability different from ordinary summability. Absolute summability is defined in a similar manner for methods involving matrix transformations of series into sequences. If the summation method is defined by a transformation of the series (2) into a series
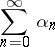 | (3) |
by means of a matrix 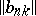 :
:
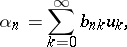 |
then the supplementary restriction is absolute convergence of the series (3). In the particular case in which the method 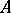 corresponds to the identity transformation of a sequence into a sequence (or of a series into a series), absolute summability of a series is the same as absolute convergence.
corresponds to the identity transformation of a sequence into a sequence (or of a series into a series), absolute summability of a series is the same as absolute convergence.
The supplementary requirements are suitably modified for non-matrix summation methods. Thus, in the case of the Abel summation method such a requirement is that the function
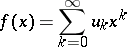 |
is of bounded variation on the semi-interval 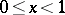 . In the case of integral summation methods, absolute summability is distinguished by the requirement of absolute convergence of the corresponding integrals. Thus, for the Borel summation method the integral
. In the case of integral summation methods, absolute summability is distinguished by the requirement of absolute convergence of the corresponding integrals. Thus, for the Borel summation method the integral
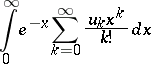 |
must be absolutely convergent.
A summation method is said to preserve absolute convergence of a series if it absolutely sums each absolutely convergent series. If each such series is summable by this method to a sum equal to the sum to which it converges, then the method is called absolutely regular. For instance, the Cesàro summation methods 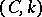 are absolutely regular for
are absolutely regular for 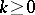 . The Abel method is absolutely regular. The following are necessary and sufficient conditions for the absolute regularity of a summation method defined by a transformation of a series into a series by means of a matrix
. The Abel method is absolutely regular. The following are necessary and sufficient conditions for the absolute regularity of a summation method defined by a transformation of a series into a series by means of a matrix 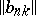 :
:
 |
(the Knopp–Lorentz theorem). Summation methods by means of other types of transformations are subject to analogous restrictions.
A generalization of absolute summability is absolute summability of degree 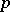 where
where 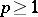 . Here the condition
. Here the condition
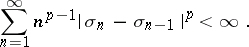 |
is the supplementary restriction by which absolute summability of degree 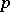 is distinguished from ordinary summability in the case of, say, a summation method defined by a transformation of a sequence
is distinguished from ordinary summability in the case of, say, a summation method defined by a transformation of a sequence 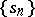 into a sequence
into a sequence  .
.
The concept of absolute summability was introduced by E. Borel for one of his methods, but was stated differently from its modern formulation: absolute summability was distinguished by imposing the condition
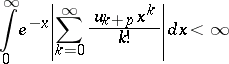 |
for each 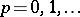 . Absolute summability was initially used in the study of the summability of power series outside the disc of convergence. In view of the problems involved in the multiplication of summable series, absolute summability was defined and studied by the method of Cesàro (
. Absolute summability was initially used in the study of the summability of power series outside the disc of convergence. In view of the problems involved in the multiplication of summable series, absolute summability was defined and studied by the method of Cesàro ( -summability). The general definition of absolute summability is more recent, and has found extensive application in studies on the summation of Fourier series.
-summability). The general definition of absolute summability is more recent, and has found extensive application in studies on the summation of Fourier series.
References
| [1] | G.H. Hardy, "Divergent series" , Clarendon Press (1949) |
| [2] | E. Kogbetliantz, "Sommation des séries et intégrales divergentes par les moyennes arithmétiques et typiques" , Gauthier-Villars (1931) |
| [3] | K. Knopp, G.G. Lorentz, "Beiträge zur absoluten Limitierung" Arch. Math. (Basel) , 2 (1949–1950) pp. 10–16 |
| [4] | G.F. Kangro, "Summability theory of series and sequences" Itogi Nauk. i Tekhn. Mat. Anal. , 12 (1974) pp. 5–70 (In Russian) |
Comments
References
| [a1] | K. Zeller, W. Beekmann, "Theorie der Limitierungsverfahren" , Springer (1970) |
Absolute summability. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Absolute_summability&oldid=15190