Absolute retract for normal spaces
A topological space  such that every mapping
such that every mapping  of any closed subset
of any closed subset  of an arbitrary normal space
of an arbitrary normal space  can be extended to the entire space
can be extended to the entire space  . A direct product of absolute retracts for normal spaces is an absolute retract for normal spaces, as is any retract (cf. Retract of a topological space) of an absolute retract for normal spaces. In particular, the following spaces are absolute retracts for normal spaces: the unit interval
. A direct product of absolute retracts for normal spaces is an absolute retract for normal spaces, as is any retract (cf. Retract of a topological space) of an absolute retract for normal spaces. In particular, the following spaces are absolute retracts for normal spaces: the unit interval  ; the
; the  -dimensional cube
-dimensional cube  ; and the Hilbert cube
; and the Hilbert cube  . Any two mappings of a binormal space into an absolute retract for normal spaces are homotopic; while a binormal absolute retract for normal spaces is contractible into a point.
. Any two mappings of a binormal space into an absolute retract for normal spaces are homotopic; while a binormal absolute retract for normal spaces is contractible into a point.
Comments
Usually an absolute retract (AR) for normal spaces is defined to be a normal space which is a retract of every normal space in which it is imbedded as a closed subset. A space satisfying the property in the article above is then called an absolute extensor (AE) for normal spaces. One then proves that a space is an (AR) if and only if it is an (AE). Absolute retracts and extensors can be defined for any class of spaces (i.e. not just for normal spaces).
A binormal space is a space 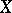 for which the product
for which the product  is normal. It can be proved that a space
is normal. It can be proved that a space  is binormal if and only if
is binormal if and only if  is normal and countably paracompact (cf. Paracompactness criteria).
is normal and countably paracompact (cf. Paracompactness criteria).
References
| [a1] | S.T. Hu, "Theory of retracts" , Wayne State Univ. Press , Detroit (1965) |
Absolute retract for normal spaces. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Absolute_retract_for_normal_spaces&oldid=32989