Abelian surface
An Abelian variety of dimension two, i.e. a complete connected group variety of dimension two over a field 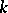 . The group law is commutative. In the sequel,
. The group law is commutative. In the sequel, 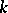 is assumed to be algebraically closed (cf. Algebraically closed field).
is assumed to be algebraically closed (cf. Algebraically closed field).
In the classification of algebraic surfaces, Abelian surfaces are exactly the smooth complete surfaces 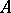 with Kodaira dimension
with Kodaira dimension 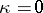 , geometric genus
, geometric genus 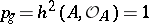 and irregularity
and irregularity 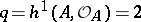 .
.
For an Abelian surface 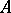 , the dual Abelian variety
, the dual Abelian variety 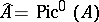 is again an Abelian surface. An invertible sheaf
is again an Abelian surface. An invertible sheaf 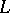 on
on 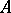 defines the homomorphism
defines the homomorphism 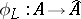 ,
, 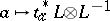 . The homomorphism
. The homomorphism 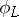 depends only on the algebraic equivalence class of
depends only on the algebraic equivalence class of 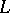 . The invertible sheaf
. The invertible sheaf 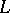 is ample (cf. Ample sheaf) if and only if
is ample (cf. Ample sheaf) if and only if 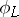 is an isogeny (i.e.,
is an isogeny (i.e., 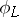 is surjective and has finite kernel) and
is surjective and has finite kernel) and 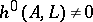 . In this case,
. In this case, 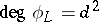 with a positive integer
with a positive integer 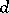 and the Riemann–Roch theorem says that
and the Riemann–Roch theorem says that
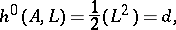 |
where 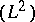 denotes the self-intersection number. Every Abelian surface admits an ample invertible sheaf and hence is projective (cf. Projective scheme).
denotes the self-intersection number. Every Abelian surface admits an ample invertible sheaf and hence is projective (cf. Projective scheme).
A polarization 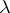 on
on 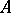 is the algebraic equivalence class
is the algebraic equivalence class 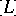 of an ample invertible sheaf
of an ample invertible sheaf 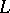 . The degree
. The degree  of
of 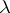 is by definition
is by definition 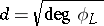 . An Abelian surface
. An Abelian surface 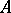 together with a polarization
together with a polarization 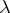 is a polarized Abelian surface. A principal polarization is a polarization of degree
is a polarized Abelian surface. A principal polarization is a polarization of degree 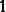 . A principally polarized Abelian surface
. A principally polarized Abelian surface 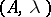 is either the Jacobi variety
is either the Jacobi variety 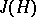 of a smooth projective curve
of a smooth projective curve 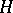 of genus
of genus  , and
, and  is the class of the theta divisor, or
is the class of the theta divisor, or 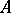 is the product of two elliptic curves (Abelian varieties of dimension one, cf. also Elliptic curve) with
is the product of two elliptic curves (Abelian varieties of dimension one, cf. also Elliptic curve) with 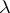 the product polarization.
the product polarization.
If the degree of  is prime to
is prime to 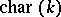 , then
, then 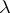 is said to be a separable polarization and the kernel of
is said to be a separable polarization and the kernel of  is isomorphic to the group
is isomorphic to the group  , where
, where  and
and 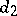 are positive integers such that
are positive integers such that 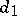 divides
divides  and
and 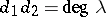 . The pair
. The pair 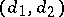 is the type of the polarized Abelian surface
is the type of the polarized Abelian surface 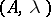 .
.
A polarization  of type
of type 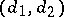 on
on 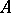 defines a polarization
defines a polarization 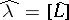 on the dual Abelian surface
on the dual Abelian surface 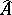 . The polarization
. The polarization 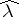 is again of type
is again of type 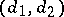 and it is characterized by each of the following two equivalent properties:
and it is characterized by each of the following two equivalent properties:
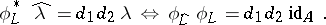 |
For a polarized Abelian surface 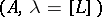 of type
of type  , the assignment
, the assignment 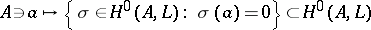 defines a rational mapping from
defines a rational mapping from 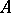 into the projective space of hyperplanes in
into the projective space of hyperplanes in 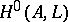 :
:
 |
If 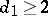 , then
, then 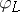 is everywhere defined. The Lefschetz theorem says that for
is everywhere defined. The Lefschetz theorem says that for 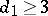 the morphism
the morphism 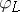 is an embedding. Suppose
is an embedding. Suppose  ; then
; then 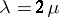 with a polarization
with a polarization  of type
of type 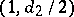 . If the linear system
. If the linear system  has no fixed components, then
has no fixed components, then 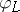 is an embedding.
is an embedding.
Complex Abelian surfaces.
An Abelian surface over the field 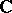 of complex numbers is a complex torus
of complex numbers is a complex torus
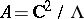 |
(with a lattice 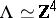 in
in  ) admitting a polarization. A polarization
) admitting a polarization. A polarization 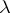 on
on 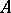 can be considered as a non-degenerate alternating form
can be considered as a non-degenerate alternating form 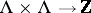 , the elementary divisors of which are given by the type
, the elementary divisors of which are given by the type  of
of 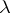 .
.
In the sequel, the field 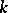 is assumed to be
is assumed to be  , although some of the following results are also valid for arbitrary algebraically closed fields.
, although some of the following results are also valid for arbitrary algebraically closed fields.
Suppose 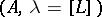 is of type
is of type 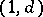 and the linear system
and the linear system  has no fixed components. The Reider theorem states that for
has no fixed components. The Reider theorem states that for 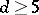 the invertible sheaf
the invertible sheaf 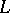 is very ample if and only if there is no elliptic curve
is very ample if and only if there is no elliptic curve 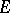 on
on 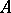 with
with 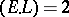 (see [a14] and [a10]). For arbitrary
(see [a14] and [a10]). For arbitrary 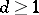 there exist finitely many isogenies
there exist finitely many isogenies 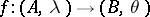 of degree
of degree 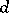 onto principally polarized Abelian surfaces (cf. also Isogeny). Suppose
onto principally polarized Abelian surfaces (cf. also Isogeny). Suppose 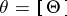 with a symmetric invertible sheaf
with a symmetric invertible sheaf 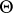 (i.e.,
(i.e., 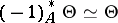 ) and let
) and let 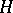 be the unique divisor in the linear system
be the unique divisor in the linear system 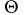 . The divisor
. The divisor 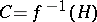 on
on 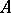 defines a symmetric invertible sheaf
defines a symmetric invertible sheaf 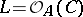 with class
with class  and the covering
and the covering 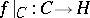 is étale of degree
is étale of degree 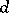 . One distinguishes two cases: i)
. One distinguishes two cases: i) 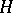 is smooth of genus
is smooth of genus  ,
, 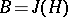 and
and 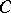 is smooth of genus
is smooth of genus 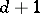 ; and ii)
; and ii) 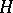 is the sum
is the sum 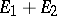 of two elliptic curves with intersection number
of two elliptic curves with intersection number 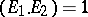 ,
, 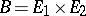 and
and 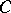 is the sum
is the sum 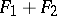 of two elliptic curves with
of two elliptic curves with 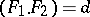 .
.
In the following list, 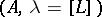 is a polarized Abelian surface of type
is a polarized Abelian surface of type 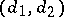 such that
such that 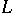 admits no fixed components
admits no fixed components
Type 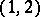 — The linear system
— The linear system 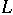 has exactly
has exactly 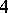 base points. The blow-up
base points. The blow-up 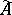 of
of 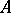 in these points admits a morphism
in these points admits a morphism 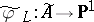 induced by
induced by 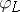 . The general fibre of
. The general fibre of 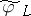 is a smooth curve of genus
is a smooth curve of genus  . The curve
. The curve 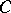 on
on 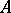 defining
defining 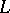 as above is double elliptic:
as above is double elliptic: 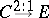 with an elliptic curve
with an elliptic curve 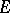 , and
, and 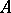 is isomorphic to
is isomorphic to 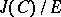 (see [a3]).
(see [a3]).
Type 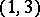 —
— 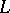 defines a
defines a 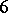 -fold covering
-fold covering 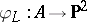 ramified along a curve
ramified along a curve 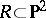 of degree
of degree 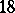 . The general divisor in the linear system
. The general divisor in the linear system 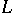 is a smooth curve of genus
is a smooth curve of genus  . There are
. There are 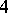 isogenies
isogenies 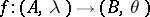 of degree
of degree  onto principally polarized Abelian surfaces. In case i) the smooth genus-
onto principally polarized Abelian surfaces. In case i) the smooth genus-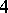 curve
curve  is double elliptic:
is double elliptic: 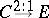 , and the embedding of
, and the embedding of 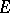 into the Jacobian
into the Jacobian 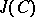 induces an exact sequence
induces an exact sequence
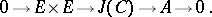 |
The étale  -fold covering
-fold covering 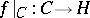 induces a morphism
induces a morphism 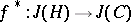 with image
with image 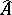 , the dual Abelian surface of
, the dual Abelian surface of 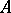 (see [a7]).
(see [a7]).
Type 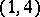 — There are
— There are 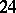 isogenies
isogenies 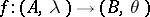 of degree
of degree 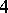 onto principally polarized Abelian surfaces. If the curves
onto principally polarized Abelian surfaces. If the curves 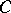 and
and 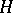 do not admit elliptic involutions compatible with
do not admit elliptic involutions compatible with 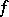 , then
, then 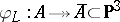 is a birational morphism onto a singular octic
is a birational morphism onto a singular octic 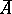 . In the exceptional case,
. In the exceptional case, 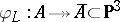 is a double covering of a singular quartic
is a double covering of a singular quartic 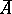 , which is birational to an elliptic scroll. In the first case the octic
, which is birational to an elliptic scroll. In the first case the octic 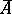 is smooth outside the four coordinate planes of
is smooth outside the four coordinate planes of 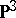 and touches the coordinate planes in curves
and touches the coordinate planes in curves 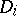 ,
, 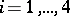 , of degree
, of degree 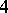 . Each of the curves
. Each of the curves 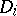 has
has  double points and passes through
double points and passes through 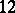 pinch points of
pinch points of 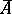 . The octic is a
. The octic is a 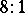 covering of a Kummer surface:
covering of a Kummer surface: 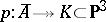 (see also Type
(see also Type 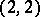 below). The restrictions
below). The restrictions 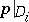 are
are 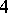 -fold coverings of four double conics of
-fold coverings of four double conics of 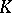 lying on a coordinate tetrahedron. The three double points of
lying on a coordinate tetrahedron. The three double points of 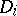 map to three double points of
map to three double points of 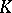 on the conic
on the conic 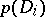 and the
and the 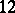 pinch points on
pinch points on 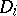 map to the other three double points on the double conic
map to the other three double points on the double conic 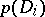 (see [a6]).
(see [a6]).
Type 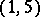 — The invertible sheaf
— The invertible sheaf 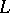 is very ample, i.e.
is very ample, i.e.  is an embedding if and only if the curves
is an embedding if and only if the curves 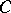 and
and 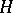 do not admit elliptic involutions compatible with
do not admit elliptic involutions compatible with 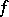 . In the exceptional case
. In the exceptional case 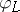 is a double covering of an elliptic scroll (see [a13] and [a9]). If
is a double covering of an elliptic scroll (see [a13] and [a9]). If  is very ample,
is very ample, 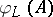 is a smooth surface of degree
is a smooth surface of degree 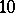 in
in 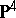 . It is the zero locus of a section of the Horrocks–Mumford bundle
. It is the zero locus of a section of the Horrocks–Mumford bundle 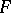 (see [a8]). Conversely, the zero set
(see [a8]). Conversely, the zero set 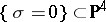 of a general section
of a general section 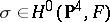 is an Abelian surface of degree
is an Abelian surface of degree 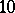 , i.e. of type
, i.e. of type  .
.
Type 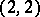 —
— 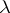 is twice a principal polarization on
is twice a principal polarization on 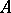 . The morphism
. The morphism 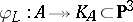 is a double covering of the Kummer surface
is a double covering of the Kummer surface 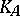 associated with
associated with 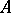 . It is isomorphic to
. It is isomorphic to 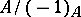 .
.
Type 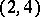 — The ideal sheaf
— The ideal sheaf 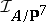 of the image of the embedding
of the image of the embedding 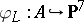 is generated by
is generated by 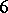 quadrics (see [a3]).
quadrics (see [a3]).
Type 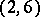 — Suppose
— Suppose 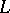 is very ample and let
is very ample and let 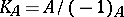 be the associated Kummer surface. The subvector space
be the associated Kummer surface. The subvector space 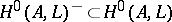 of odd sections induces an embedding of
of odd sections induces an embedding of 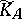 , the blow-up of
, the blow-up of 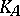 in the
in the 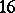 double points, as a smooth quartic surface into
double points, as a smooth quartic surface into 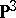 .
. 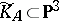 is invariant under the action of the level-
is invariant under the action of the level- Heisenberg group (cf. also Heisenberg representation)
Heisenberg group (cf. also Heisenberg representation) 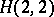 . The
. The 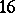 blown-up double points become skew lines on the quartic surface. Any
blown-up double points become skew lines on the quartic surface. Any 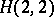 -invariant quartic surface in
-invariant quartic surface in 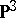 with
with 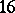 skew lines comes from a polarized Abelian surface
skew lines comes from a polarized Abelian surface 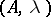 of type
of type  in this way (see [a5], [a11] and [a12]).
in this way (see [a5], [a11] and [a12]).
Type 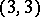 —
— 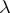 is three times a principal polarization and
is three times a principal polarization and  is an embedding. If
is an embedding. If 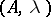 is not a product, then the quadrics
is not a product, then the quadrics 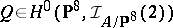 vanishing on
vanishing on 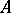 generate the ideal sheaf
generate the ideal sheaf 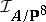 . In the product case,
. In the product case,  is generated by quadrics and cubics (see [a4]).
is generated by quadrics and cubics (see [a4]).
Algebraic completely integrable systems.
An algebraic completely integrable system in the sense of M. Adler and P. van Moerbeke is a completely integrable polynomial Hamiltonian system on 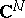 (with Casimir functions
(with Casimir functions 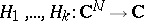 and
and 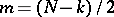 independent constants of motion
independent constants of motion 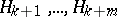 in involution) such that:
in involution) such that:
a) for a general point 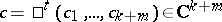 the invariant manifold
the invariant manifold 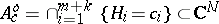 is an open affine part of an Abelian variety
is an open affine part of an Abelian variety 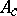 ;
;
b) the flows of the integrable vector fields 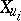 linearize on the Abelian varieties
linearize on the Abelian varieties 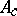 [a2].
[a2].
The divisor at infinity 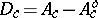 defines a polarization on
defines a polarization on 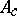 . In this way the mapping
. In this way the mapping 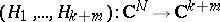 defines a family of polarized Abelian varieties (cf. Moduli problem). Some examples of
defines a family of polarized Abelian varieties (cf. Moduli problem). Some examples of  -dimensional algebraic completely integrable systems and their associated Abelian surfaces are:
-dimensional algebraic completely integrable systems and their associated Abelian surfaces are:
the three-body Toda lattice and the even, respectively odd, master systems (cf. also Master equations in cooperative and social phenomena) linearize on principally polarized Abelian surfaces;
the Kowalewski top, the Hénon–Heiles system and the Manakov geodesic flow on 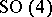 linearize on Abelian surfaces of type
linearize on Abelian surfaces of type 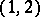 [a1];
[a1];
the Garnier system linearizes on Abelian surfaces of type 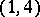 [a15].
[a15].
References
| [a1] | M. Adler, P. van Moerbeke, "The Kowalewski and Hénon–Heiles motions as Manakov geodesic flows on 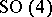 : a two-dimensional family of Lax pairs" Comm. Math. Phys. , 113 (1988) pp. 659–700 : a two-dimensional family of Lax pairs" Comm. Math. Phys. , 113 (1988) pp. 659–700 |
| [a2] | M. Adler, P. van Moerbeke, "The complex geometry of the Kowalewski–Painlevé analysis" Invent. Math. , 97 (1989) pp. 3–51 |
| [a3] | W. Barth, "Abelian surfaces with 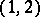 -polarization" , Algebraic Geometry, Sendai, 1985 , Advanced Studies in Pure Math. , 10 (1987) pp. 41–84 -polarization" , Algebraic Geometry, Sendai, 1985 , Advanced Studies in Pure Math. , 10 (1987) pp. 41–84 |
| [a4] | W. Barth, "Quadratic equations for level- abelian surfaces" , Abelian Varieties, Proc. Workshop Egloffstein 1993 , de Gruyter (1995) pp. 1–18 abelian surfaces" , Abelian Varieties, Proc. Workshop Egloffstein 1993 , de Gruyter (1995) pp. 1–18 |
| [a5] | W. Barth, I. Nieto, "Abelian surfaces of type 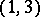 and quartic surfaces with and quartic surfaces with 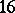 skew lines" J. Algebraic Geom. , 3 (1994) pp. 173–222 skew lines" J. Algebraic Geom. , 3 (1994) pp. 173–222 |
| [a6] | Ch. Birkenhake, H. Lange, D. van Straten, "Abelian surfaces of type 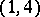 " Math. Ann. , 285 (1989) pp. 625–646 " Math. Ann. , 285 (1989) pp. 625–646 |
| [a7] | Ch. Birkenhake, H. Lange, "Moduli spaces of Abelian surfaces wih isogeny" , Geometry and Analysis, Bombay Colloquium 1992 , Tata Inst. Fundam. Res. (1995) pp. 225–243 |
| [a8] | G. Horrocks, D. Mumford, "A rank  vector bundle on vector bundle on 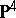 with with 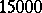 symmetries" Topology , 12 (1973) pp. 63–81 symmetries" Topology , 12 (1973) pp. 63–81 |
| [a9] | K. Hulek, H. Lange, "Examples of abelian surfaces in 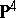 " J. Reine Angew. Math. , 363 (1985) pp. 200–216 " J. Reine Angew. Math. , 363 (1985) pp. 200–216 |
| [a10] | H. Lange, Ch. Birkenhake, "Complex Abelian varieties" , Grundlehren math. Wiss. , 302 , Springer (1992) |
| [a11] | I. Naruki, "On smooth quartic embeddings of Kummer surfaces" Proc. Japan Acad. , 67 A (1991) pp. 223–224 |
| [a12] | V. V. Nikulin, "On Kummer surfaces" Math USSR Izv. , 9 (1975) pp. 261–275 (In Russian) |
| [a13] | S. Ramanan, "Ample divisors on abelian surfaces" Proc. London Math. Soc. , 51 (1985) pp. 231–245 |
| [a14] | I. Reider, "Vector bundles of rank  and linear systems on algebraic surfaces" Ann. of Math. , 127 (1988) pp. 309–316 and linear systems on algebraic surfaces" Ann. of Math. , 127 (1988) pp. 309–316 |
| [a15] | P. Vanhaecke, "A special case of the Garnier system, 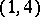 -polarized Abelian surfaces and their moduli" Compositio Math. , 92 (1994) pp. 157–203 -polarized Abelian surfaces and their moduli" Compositio Math. , 92 (1994) pp. 157–203 |
Abelian surface. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Abelian_surface&oldid=16005