Abelian integral
algebraic integral
An integral of an algebraic function, i.e. an integral of the form
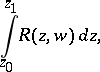 | (1) |
where 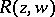 is some rational function in variables
is some rational function in variables  that are related by an algebraic equation
that are related by an algebraic equation
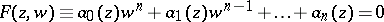 | (2) |
with coefficients 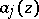 that are polynomials in
that are polynomials in  ,
, 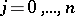 . To equation (2) there corresponds a compact Riemann surface
. To equation (2) there corresponds a compact Riemann surface 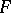 which is an
which is an  -sheeted covering of the Riemann sphere. On this Riemann surface
-sheeted covering of the Riemann sphere. On this Riemann surface 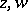 , and consequently also
, and consequently also 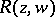 , can be considered as single-valued functions of the points on
, can be considered as single-valued functions of the points on 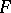 .
.
The integral (1) is then given as the integral 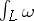 of the Abelian differential
of the Abelian differential 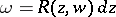 on
on 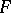 taken along some rectifiable path
taken along some rectifiable path  . In general, specifying only the initial and end points
. In general, specifying only the initial and end points 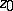 and
and 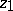 of the path
of the path 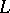 does not completely determine the value of the Abelian integral (1), or, which is the same, the integral (1) turns out to be a multi-valued function of the initial and end points of the path
does not completely determine the value of the Abelian integral (1), or, which is the same, the integral (1) turns out to be a multi-valued function of the initial and end points of the path 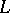 .
.
The behaviour of an Abelian integral on 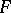 depends, first of all, on the topological structure of
depends, first of all, on the topological structure of 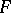 , in particular on the topological invariant called the genus
, in particular on the topological invariant called the genus 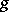 of the surface
of the surface 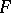 (cf. Genus of a surface). The genus
(cf. Genus of a surface). The genus 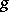 is connected with the number of sheets
is connected with the number of sheets  and with the number of branch points
and with the number of branch points  (counted with multiplicities) by the relation
(counted with multiplicities) by the relation 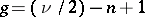 . For
. For 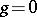 the variables
the variables  and
and 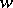 can be rationally expressed in some parameter
can be rationally expressed in some parameter  , and the Abelian integral becomes the integral of a rational function in
, and the Abelian integral becomes the integral of a rational function in 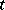 . This will happen, for example, in the elementary cases
. This will happen, for example, in the elementary cases 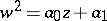 and
and 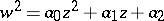 .
.
If 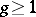 , any Abelian integral can be expressed in the form of a linear combination of elementary functions and canonical Abelian integrals of the three kinds. The integral
, any Abelian integral can be expressed in the form of a linear combination of elementary functions and canonical Abelian integrals of the three kinds. The integral 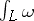 is called an Abelian integral of the first kind if
is called an Abelian integral of the first kind if 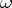 is an Abelian differential of the first kind. In other words, Abelian integrals of the first kind are characterized by the fact that for a fixed initial point
is an Abelian differential of the first kind. In other words, Abelian integrals of the first kind are characterized by the fact that for a fixed initial point 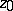 of the path
of the path 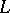 they are a function of the upper bound
they are a function of the upper bound 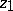 that is an everywhere finite, usually multi-valued, function on
that is an everywhere finite, usually multi-valued, function on 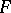 . Such a characterization may be used, for example, to construct analogues of Abelian integrals of the first kind on non-compact Riemann surfaces. Any Abelian integral of the first kind can be represented in the form of a linear combination of
. Such a characterization may be used, for example, to construct analogues of Abelian integrals of the first kind on non-compact Riemann surfaces. Any Abelian integral of the first kind can be represented in the form of a linear combination of 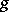 linearly-independent normal Abelian integrals of the first kind
linearly-independent normal Abelian integrals of the first kind
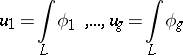 |
of differentials 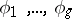 that constitute a canonical basis for the Abelian differentials of the first kind. If the surface
that constitute a canonical basis for the Abelian differentials of the first kind. If the surface 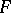 is cut along the cycles
is cut along the cycles 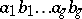 of a canonical basis for the homology, a simply-connected domain
of a canonical basis for the homology, a simply-connected domain 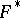 is obtained. The integrals
is obtained. The integrals 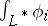 are single-valued functions of the upper bound
are single-valued functions of the upper bound 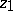 for all paths
for all paths 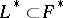 with fixed initial point
with fixed initial point 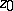 and fixed end point
and fixed end point  . The multi-valuedness of the integrals
. The multi-valuedness of the integrals 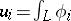 along an arbitrary path
along an arbitrary path 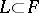 joining
joining  with
with 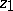 is now completely described by the fact that it differs from the integrals
is now completely described by the fact that it differs from the integrals 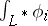 only by an integral linear combination of the
only by an integral linear combination of the 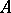 -periods
-periods 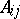 and the
and the 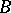 -periods
-periods 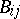 of a basis of the differentials of the first kind. These constitute the period matrix of dimension
of a basis of the differentials of the first kind. These constitute the period matrix of dimension 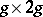 , which satisfies the bilinear Riemann relations (cf. Abelian differential).
, which satisfies the bilinear Riemann relations (cf. Abelian differential).
An integral  where
where 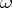 is an Abelian differential of the second kind is said to be an Abelian integral of the second kind. Considered as a function of the upper bound, it has no singularities anywhere on
is an Abelian differential of the second kind is said to be an Abelian integral of the second kind. Considered as a function of the upper bound, it has no singularities anywhere on 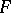 except for poles. An Abelian integral of a normalized Abelian differential of the second kind is known as a normal Abelian integral of the second kind.
except for poles. An Abelian integral of a normalized Abelian differential of the second kind is known as a normal Abelian integral of the second kind.
An Abelian integral of the third kind is an arbitrary Abelian integral. It usually has logarithmic singularities on 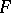 ; however, such singularities can only occur in pairs. An Abelian integral of a normal Abelian differential of the third kind is called a normal Abelian integral of the third kind. Any Abelian integral can be represented as a linear combination of normal Abelian integrals of the first, second and third kinds. Unlike Abelian integrals of the first and second kinds, Abelian integrals of the third kind usually also have the so-called polar periods, beside the
; however, such singularities can only occur in pairs. An Abelian integral of a normal Abelian differential of the third kind is called a normal Abelian integral of the third kind. Any Abelian integral can be represented as a linear combination of normal Abelian integrals of the first, second and third kinds. Unlike Abelian integrals of the first and second kinds, Abelian integrals of the third kind usually also have the so-called polar periods, beside the 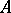 - and
- and 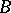 -periods (which are called cyclic periods). Polar periods are taken along cycles which are homologous to zero, but encircle the logarithmic singularities of the Abelian integral. They are caused by the poles of the Abelian differential
-periods (which are called cyclic periods). Polar periods are taken along cycles which are homologous to zero, but encircle the logarithmic singularities of the Abelian integral. They are caused by the poles of the Abelian differential 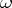 with non-zero residues.
with non-zero residues.
A number of relations depending on the topological and conformal structure of 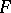 exist for arbitrary Abelian integrals on the same Riemann surface
exist for arbitrary Abelian integrals on the same Riemann surface 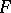 . Thus, if
. Thus, if 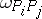 is a normal Abelian differential of the third kind with simple poles in
is a normal Abelian differential of the third kind with simple poles in 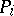 and
and 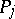 , then the following theorem on the permutation of the parameters and the bounds of an Abelian integral of the third kind holds for all points
, then the following theorem on the permutation of the parameters and the bounds of an Abelian integral of the third kind holds for all points 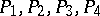 :
:
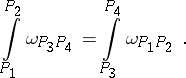 |
Relations which connect Abelian integrals with rational functions on 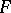 are known as Abelian theorems. In terms of divisors, for example, the Abelian theorem for Abelian integrals of the first kind has the following form: A divisor
are known as Abelian theorems. In terms of divisors, for example, the Abelian theorem for Abelian integrals of the first kind has the following form: A divisor  on
on 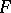 is the divisor of a meromorphic function if and only if there exists a chain
is the divisor of a meromorphic function if and only if there exists a chain 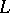 with
with 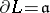 and
and 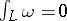 for all Abelian differentials of the first kind on
for all Abelian differentials of the first kind on  . There also exist variants of Abelian theorems for Abelian integrals of the second and third kinds [4]. Abelian integrals and, in particular, Abelian theorems, are the basis of the transcendental construction of the Jacobi variety of a Riemann surface. The question of the inversion of an Abelian integral as a function of its upper bound also leads to the concepts of an Abelian function; an elliptic function; and theta-functions (cf. Theta-function; Jacobi inversion problem).
. There also exist variants of Abelian theorems for Abelian integrals of the second and third kinds [4]. Abelian integrals and, in particular, Abelian theorems, are the basis of the transcendental construction of the Jacobi variety of a Riemann surface. The question of the inversion of an Abelian integral as a function of its upper bound also leads to the concepts of an Abelian function; an elliptic function; and theta-functions (cf. Theta-function; Jacobi inversion problem).
Historically, the theory of Abelian integrals followed from the consideration of a surface of genus 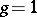 . If one writes the corresponding equation in the form
. If one writes the corresponding equation in the form
 |
where 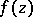 is a polynomial in
is a polynomial in  of the third or fourth degree, then one obtains elliptic integrals (cf. Elliptic integral) as the respective Abelian integrals. They first appeared at the end of the 17th century and the beginning of the 18th century as the result of the rectification of curves of the second order in the studies of Jacob and Johann Bernoulli and of G. Fagnano. L. Euler tackled the addition theorem of elliptic integrals, which is a special case of a theorem of N.H. Abel (1752). Abel and C.G.J. Jacobi (1827) stated the problem of inversion of elliptic integrals and obtained the solution. The beginnings of the theory of elliptic functions were thus established. However, some facts concerning this theory had been established by C.F. Gauss early in the 18th century. Abel and Jacobi dealt with the much more difficult case of inversion of Abelian integrals in the case
of the third or fourth degree, then one obtains elliptic integrals (cf. Elliptic integral) as the respective Abelian integrals. They first appeared at the end of the 17th century and the beginning of the 18th century as the result of the rectification of curves of the second order in the studies of Jacob and Johann Bernoulli and of G. Fagnano. L. Euler tackled the addition theorem of elliptic integrals, which is a special case of a theorem of N.H. Abel (1752). Abel and C.G.J. Jacobi (1827) stated the problem of inversion of elliptic integrals and obtained the solution. The beginnings of the theory of elliptic functions were thus established. However, some facts concerning this theory had been established by C.F. Gauss early in the 18th century. Abel and Jacobi dealt with the much more difficult case of inversion of Abelian integrals in the case  . During the very first stages of development stress was laid on hyper-elliptic integrals, where
. During the very first stages of development stress was laid on hyper-elliptic integrals, where  with
with 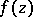 a polynomial of the fifth or sixth degree without multiple roots. Here
a polynomial of the fifth or sixth degree without multiple roots. Here 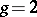 and the difficulty of the inversion problem can already be noticed. The principal advances in the theory of inversion of Abelian integrals are due to B. Riemann (1851), who introduced the concept of Riemann surfaces and formulated and gave proofs of a large number of important results.
and the difficulty of the inversion problem can already be noticed. The principal advances in the theory of inversion of Abelian integrals are due to B. Riemann (1851), who introduced the concept of Riemann surfaces and formulated and gave proofs of a large number of important results.
Multi-dimensional generalizations of the theory of Abelian integrals form the subject matter of algebraic geometry and the theory of complex manifolds.
References
| [1] | N.G. Chebotarev, "The theory of algebraic functions" , Moscow-Leningrad (1948) pp. Chapt.8;9 (In Russian) |
| [2] | G. Springer, "Introduction to Riemann surfaces" , Addison-Wesley (1957) pp. Chapt.10 |
| [3] | R. Nevanlinna, "Uniformisierung" , Springer (1953) pp. Chapt.5 |
| [4] | G.A. Bliss, "Algebraic functions" , Amer. Math. Soc. (1933) |
| [5] | H. Stahl, "Theorie der Abelschen Funktionen" , Leipzig (1896) |
| [6] | I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) |
Comments
An interesting and useful additional reference is [a1].
References
| [a1] | S. Lang, "Introduction to algebraic and Abelian functions" , Addison-Wesley (1972) |
Abelian integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Abelian_integral&oldid=13186