Abelian differential
A holomorphic or meromorphic differential on a compact, or closed, Riemann surface 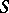 (cf. Differential on a Riemann surface).
(cf. Differential on a Riemann surface).
Let 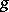 be the genus of the surface
be the genus of the surface 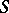 (cf. Genus of a surface); let
(cf. Genus of a surface); let 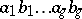 be the cycles of a canonical basis of the homology of
be the cycles of a canonical basis of the homology of 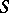 . Depending on the nature of their singular points, one distinguishes three kinds of Abelian differentials: I, II and III, with proper inclusions
. Depending on the nature of their singular points, one distinguishes three kinds of Abelian differentials: I, II and III, with proper inclusions 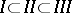 . Abelian differentials of the first kind are first-order differentials that are holomorphic everywhere on
. Abelian differentials of the first kind are first-order differentials that are holomorphic everywhere on 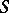 and that, in a neighbourhood
and that, in a neighbourhood 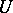 of each point
of each point 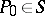 , have the form
, have the form 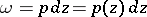 , where
, where 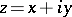 is a local uniformizing variable in
is a local uniformizing variable in 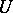 ,
, 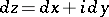 , and
, and 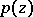 is a holomorphic, or regular, analytic function of
is a holomorphic, or regular, analytic function of  in
in 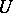 . The addition of Abelian differentials and multiplication by a holomorphic function are defined by natural rules: If
. The addition of Abelian differentials and multiplication by a holomorphic function are defined by natural rules: If
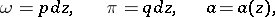 |
then
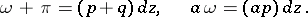 |
The Abelian differentials of the first kind form a 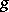 -dimensional vector space
-dimensional vector space 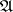 . After the introduction of the scalar product
. After the introduction of the scalar product
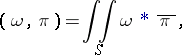 |
where  is the exterior product of
is the exterior product of 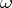 with the star-conjugate differential
with the star-conjugate differential 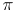 , the space
, the space 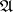 becomes a Hilbert space.
becomes a Hilbert space.
Let 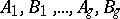 be the
be the 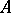 - and
- and 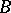 -periods of the Abelian differential of the first kind
-periods of the Abelian differential of the first kind 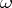 , i.e. the integrals
, i.e. the integrals
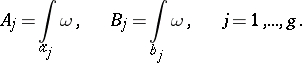 |
The following relation then holds:
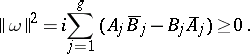 | (1) |
If 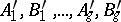 are the periods of another Abelian differential of the first kind
are the periods of another Abelian differential of the first kind 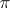 , then one has
, then one has
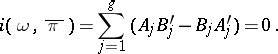 | (2) |
The relations (1) and (2) are known as the bilinear Riemann relations for Abelian differentials of the first kind. A canonical basis of the Abelian differentials of the first kind, i.e. a canonical basis 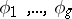 of the space
of the space 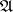 , can be chosen so that
, can be chosen so that
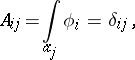 |
where  and
and 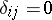 if
if  . The matrix
. The matrix  ,
, 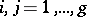 , of the
, of the 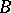 -periods
-periods
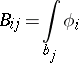 |
is then symmetric, and the matrix of the imaginary parts 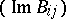 is positive definite. An Abelian differential of the first kind for which all the
is positive definite. An Abelian differential of the first kind for which all the 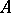 -periods or all the
-periods or all the 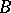 -periods are zero is identically equal to zero. If all the periods of an Abelian differential of the first kind
-periods are zero is identically equal to zero. If all the periods of an Abelian differential of the first kind 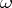 are real, then
are real, then 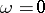 .
.
Abelian differentials of the second and third kinds are, in general, meromorphic differentials, i.e. analytic differentials which have on 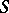 not more than a finite set of singular points that are poles and which have local representations
not more than a finite set of singular points that are poles and which have local representations
 | (3) |
where 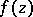 is a regular function,
is a regular function,  is the order of the pole (if
is the order of the pole (if 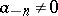 ), and
), and 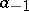 is the residue of the pole. If
is the residue of the pole. If 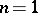 , the pole is said to be simple. An Abelian differential of the second kind is a meromorphic differential all residues of which are zero, i.e. a meromorphic differential with local representation
, the pole is said to be simple. An Abelian differential of the second kind is a meromorphic differential all residues of which are zero, i.e. a meromorphic differential with local representation
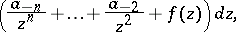 |
An Abelian differential of the third kind is an arbitrary Abelian differential.
Let 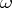 be an arbitrary Abelian differential with
be an arbitrary Abelian differential with 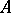 -periods
-periods 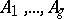 ; the Abelian differential
; the Abelian differential 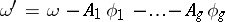 then has zero
then has zero 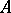 -periods and is known as a normalized Abelian differential. In particular, if
-periods and is known as a normalized Abelian differential. In particular, if 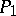 and
and 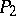 are any two points on
are any two points on 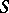 , one can construct a normalized Abelian differential
, one can construct a normalized Abelian differential 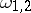 with the singularities
with the singularities 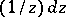 in
in 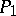 and
and 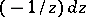 in
in 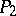 , which is known as a normal Abelian differential of the third kind. Let
, which is known as a normal Abelian differential of the third kind. Let  be an arbitrary Abelian differential with residues
be an arbitrary Abelian differential with residues  at the respective points
at the respective points 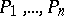 ; then, always,
; then, always, 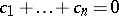 . If
. If 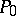 is any arbitrary point on
is any arbitrary point on 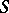 such that
such that 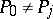 ,
, 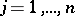 , then
, then 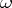 can be represented as a linear combination of a normalized Abelian differential of the second kind
can be represented as a linear combination of a normalized Abelian differential of the second kind 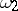 , a finite number of normal Abelian differentials of the third kind
, a finite number of normal Abelian differentials of the third kind 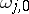 , and basis Abelian differentials of the first kind
, and basis Abelian differentials of the first kind 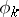 :
:
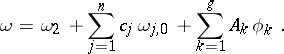 |
Let 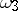 be an Abelian differential of the third kind with only simple poles with residues
be an Abelian differential of the third kind with only simple poles with residues 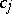 at the points
at the points 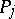 ,
, 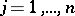 , and let
, and let 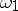 be an arbitrary Abelian differential of the first kind:
be an arbitrary Abelian differential of the first kind:
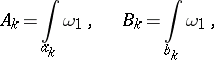 |
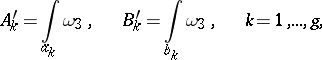 |
where the cycles 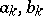 do not pass through the poles of
do not pass through the poles of 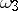 . Let the point
. Let the point 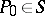 not lie on the cycles
not lie on the cycles 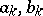 and let
and let 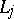 be a path from
be a path from 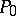 to
to 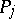 . One then obtains bilinear relations for Abelian differentials of the first and third kinds:
. One then obtains bilinear relations for Abelian differentials of the first and third kinds:
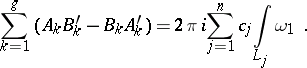 |
Bilinear relations of a similar type also exist between Abelian differentials of the first and second kinds.
In addition to the 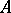 - and
- and 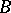 -periods
-periods 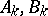 ,
, 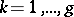 , known as the cyclic periods, an arbitrary Abelian differential of the third kind also has polar periods of the form
, known as the cyclic periods, an arbitrary Abelian differential of the third kind also has polar periods of the form 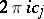 along zero-homologous cycles which encircle the poles
along zero-homologous cycles which encircle the poles 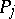 . One thus has, for an arbitrary cycle
. One thus has, for an arbitrary cycle 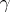 ,
,
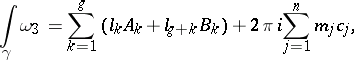 |
where 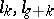 , and
, and 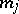 are integers.
are integers.
Important properties of Abelian differentials are described in terms of divisors. Let 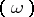 be the divisor of the Abelian differential
be the divisor of the Abelian differential 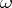 , i.e.
, i.e. 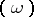 is an expression of the type
is an expression of the type 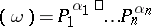 , where the
, where the 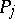 -s are all the zeros and poles of
-s are all the zeros and poles of 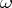 and where the
and where the 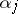 -s are their multiplicities or orders. The degree
-s are their multiplicities or orders. The degree 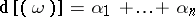 of the divisor of the Abelian differential
of the divisor of the Abelian differential 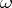 depends only on the genus of
depends only on the genus of 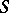 , and one always has
, and one always has 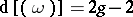 . Let
. Let  be some given divisor. Let
be some given divisor. Let 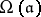 denote the complex vector space of Abelian differentials
denote the complex vector space of Abelian differentials 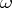 of which the divisors
of which the divisors 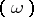 are multiples of
are multiples of  , and let
, and let 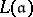 denote the vector space of meromorphic functions
denote the vector space of meromorphic functions 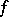 on
on 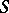 of which the divisors
of which the divisors  are multiples of
are multiples of  . Then
. Then 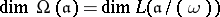 . Other important information on the dimension of these spaces is contained in the Riemann–Roch theorem: The equality
. Other important information on the dimension of these spaces is contained in the Riemann–Roch theorem: The equality
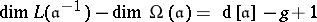 |
is valid for any divisor  . It follows from the above, for example, that if
. It follows from the above, for example, that if 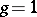 , i.e. on the surface of a torus, a meromorphic function cannot have a single simple pole.
, i.e. on the surface of a torus, a meromorphic function cannot have a single simple pole.
Let 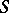 be an arbitrary compact Riemann surface on which there are meromorphic functions
be an arbitrary compact Riemann surface on which there are meromorphic functions  and
and 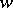 which satisfy an irreducible algebraic equation
which satisfy an irreducible algebraic equation 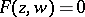 . Any arbitrary Abelian differential on
. Any arbitrary Abelian differential on 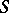 can then be expressed as
can then be expressed as 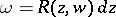 where
where 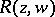 is some rational function in
is some rational function in  and
and 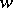 ; conversely, the expression
; conversely, the expression 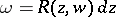 is an Abelian differential. This means that an arbitrary Abelian integral
is an Abelian differential. This means that an arbitrary Abelian integral
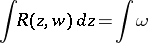 |
is the integral of some Abelian differential on a compact Riemann surface 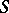 .
.
See also Algebraic function.
References
| [1] | G. Springer, "Introduction to Riemann surfaces" , Addison-Wesley (1957) pp. Chapt.10 |
| [2] | R. Nevanlinna, "Uniformisierung" , Springer (1953) pp. Chapt.5 |
| [3] | N.G. Chebotarev, "The theory of algebraic functions" , Moscow-Leningrad (1948) pp. Chapt.3;8 (In Russian) |
Comments
Another good reference, replacing [3], is [a1].
References
| [a1] | S. Lang, "Introduction to algebraic and abelian functions" , Addison-Wesley (1972) |
Abelian differential. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Abelian_differential&oldid=17348