Abel problem
To find, in a vertical plane  , a curve such that a material point moving along it under gravity from rest, starting from a point with ordinate
, a curve such that a material point moving along it under gravity from rest, starting from a point with ordinate  , will meet the
, will meet the  -axis after a time
-axis after a time 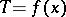 , where the function
, where the function 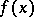 is given in advance. The problem was posed by N.H. Abel in 1823, and its solution involves one of the first integral equations — the Abel integral equation — which was also solved. In fact, if
is given in advance. The problem was posed by N.H. Abel in 1823, and its solution involves one of the first integral equations — the Abel integral equation — which was also solved. In fact, if 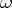 is the angle formed by the tangent of the curve being sought with the
is the angle formed by the tangent of the curve being sought with the  -axis, then
-axis, then
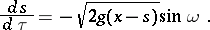 |
Integrating this equation between  and
and  and putting
and putting
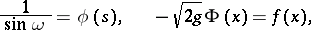 |
one obtains the integral equation
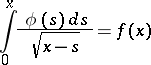 |
for the unknown function 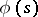 , the determination of which makes it possible to find the equation of the curve being sought. The solution of the equation introduced above is:
, the determination of which makes it possible to find the equation of the curve being sought. The solution of the equation introduced above is:
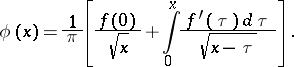 |
References
| [1] | N.H. Abel, "Solutions de quelques problèmes à l'aide d'intégrales défines" , Oeuvres complètes, nouvelle éd. , 1 , Grondahl & Son , Christiania (1881) pp. 11–27 (Edition de Holmboe) |
Comments
In the case that 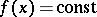 , this is the famous tautochrone problem first solved by Chr. Huyghens, who showed that this curve is then a cycloid.
, this is the famous tautochrone problem first solved by Chr. Huyghens, who showed that this curve is then a cycloid.
References
| [a1] | A.J. Jerri, "Introduction to integral equations with applications" , M. Dekker (1985) pp. Sect. 2.3 |
| [a2] | H. Hochstadt, "Integral equations" , Wiley (1973) |
| [a3] | B.L. Moiseiwitsch, "Integral equations" , Longman (1977) |
Abel problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Abel_problem&oldid=12327