Abel-Poisson summation method
One of the methods for summing Fourier series. The Fourier series of a function 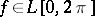 is summable by the Abel–Poisson method at a point
is summable by the Abel–Poisson method at a point  to a number
to a number  if
if
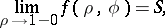 |
where
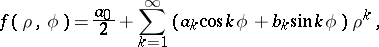 |
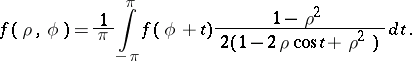 | (*) |
If  , then the integral on the right-hand side is a harmonic function for
, then the integral on the right-hand side is a harmonic function for  , which is, as has been shown by S. Poisson, a solution of the Dirichlet problem for the disc. The Abel summation method applied to Fourier series was therefore named the Abel–Poisson summation method, and the integral (*) was named the Poisson integral.
, which is, as has been shown by S. Poisson, a solution of the Dirichlet problem for the disc. The Abel summation method applied to Fourier series was therefore named the Abel–Poisson summation method, and the integral (*) was named the Poisson integral.
If  are polar coordinates of a point inside the disc of radius one, then one can consider the limit of
are polar coordinates of a point inside the disc of radius one, then one can consider the limit of 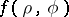 as the point
as the point 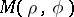 approaches a point on the bounding circle not by a radial or by a tangential but rather along an arbitrary path. In this situation the Schwarz theorem applies: If
approaches a point on the bounding circle not by a radial or by a tangential but rather along an arbitrary path. In this situation the Schwarz theorem applies: If 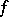 belongs to
belongs to 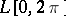 and is continuous at a point
and is continuous at a point 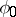 , then
, then
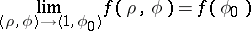 |
irrespective of the path along which the point 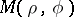 approaches the point
approaches the point 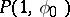 as long as that path remains within the disc with radius one.
as long as that path remains within the disc with radius one.
References
| [1] | N.K. [N.K. Bari] Bary, "A treatise on trigonometric series" , Pergamon (1964) (Translated from Russian) |
Comments
A theorem related to Schwarz' theorem stated above is Fatou's theorem: If 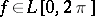 , then for almost all
, then for almost all 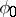
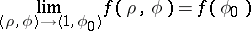 |
as 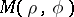 approaches
approaches 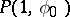 non-tangentially inside the disc, cf. [a2], pp. 129-130.
non-tangentially inside the disc, cf. [a2], pp. 129-130.
References
| [a1] | A. Zygmund, "Trigonometric series" , 1–2 , Cambridge Univ. Press (1988) |
| [a2] | M. Tsuji, "Potential theory in modern function theory" , Maruzen (1975) |
Abel-Poisson summation method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Abel-Poisson_summation_method&oldid=18630