A priori distribution
The probability distribution of a random variable, to be contrasted with the conditional distribution of this random variable under certain additional conditions. Usually the term "a priori distribution" is used in the following way. Let 
be a pair of random variables (random vectors or more general random elements). The random variable 
is considered to be unknown, while 
is considered to be the result of an observation to be used for estimation of 
. The joint distribution of 
and 
is given by the distribution of 
(now called the a priori distribution) and the set of conditional probabilities 
of the random variable 
given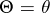 
. According to the Bayes formula, one can calculate the conditional probability of 
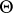with respect to 
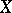(which is now called the a posteriori distribution of 
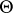). In statistical problems, the a priori distribution is often unknown (and even the assumption on its existence is not sufficiently founded). For the use of the a priori distribution, see Bayesian approach.
Comments
References
| [a1] | E. Sverdrup, "Laws and chance variations" , 1 , North-Holland (1967) pp. 214ff |
A priori distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=A_priori_distribution&oldid=12611