A-set

analytic set, in a complete separable metric space

A continuous image of a Borel set. Since any Borel set is a continuous image of the set of irrational numbers, an -set can be defined as a continuous image of the set of irrational numbers. A countable intersection and a countable union of -sets is an -set. Any -set is Lebesgue-measurable. The property of being an -set is invariant relative to Borel-measurable mappings, and to -operations (cf. -operation). Moreover, for a set to be an -set it is necessary and sufficient that it can be represented as the result of an -operation applied to a family of closed sets. There are examples of 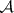-sets which are not Borel sets; thus, in the space of all closed subsets of the unit interval of the real numbers, the set of all closed uncountable sets is an -set, but is not Borel. Any uncountable -set topologically contains a perfect Cantor set. Thus, 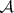-sets "realize" the continuum hypothesis: their cardinality is either finite, or . The Luzin separability principles hold for -sets.

References

[1]	K. Kuratowski, "Topology" , 1 , Acad. Press (1966) (Translated from French)
[2]	N.N. [N.N. Luzin] Lusin, "Leçons sur les ensembles analytiques et leurs applications" , Gauthier-Villars (1930)

Comments

Nowadays the class of analytic sets is denoted by 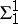, and the class of co-analytic sets (cf. -set) by .

References

[a1]	T.J. Jech, "The axiom of choice" , North-Holland (1973)
[a2]	Y.N. Moschovakis, "Descriptive set theory" , North-Holland (1980)