A-integral
From Encyclopedia of Mathematics
One of the generalizations of the Lebesgue integral, given by E. Titchmarsh [1] for the integration of functions conjugate to summable ones. A measurable function 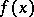 is called
is called 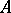 -integrable over
-integrable over 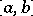 if
if
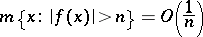 |
and if
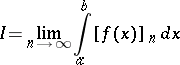 |
exists, where
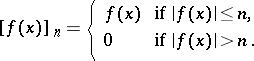 |
The number 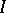 is called the
is called the  -integral. It is denoted by
-integral. It is denoted by
 |
References
| [1] | E.G. Titchmarsh, "On conjugate functions" Proc. London Math. Soc. , 29 (1928) pp. 49–80 |
| [2] | I.A. Vinogradova, "Generalized integrals and Fourier series" Itogi Nauk. Mat. Anal. 1970 (1971) pp. 65–107 (In Russian) |
How to Cite This Entry:
A-integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=A-integral&oldid=34099
A-integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=A-integral&oldid=34099
This article was adapted from an original article by I.A. Vinogradova (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article