Inscribed and circumscribed figures
A polygon is said to be inscribed in a convex curve, while the curve is said to circumscribe the polygon, if all vertices of the polygon lie on the curve (Fig. a).
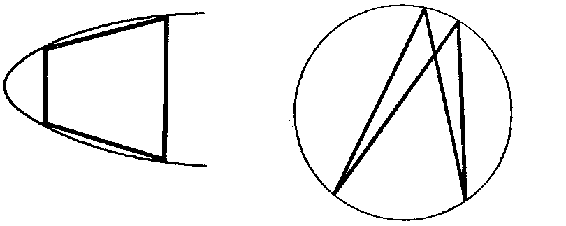
Figure: i051250a
A polygon is said to be circumscribed about a convex curve, while the curve is said to inscribe (or externally inscribe, escribe) the polygon, if all sides of the polygon (extended if necessary) are tangent to the curve. The curve most frequently considered in this connection is a circle. For instance, any triangle has one circumscribed circle and four inscribed circles, three of which are externally inscribed (Fig. b).
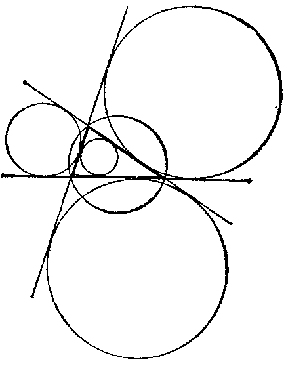
Figure: i051250b
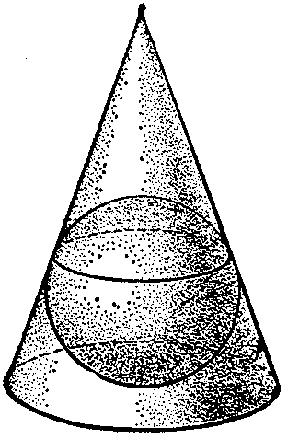
Figure: i051250c
Inscribed and circumscribed figures are also considered in space. In such a case the polygon is replaced by a polyhedron, while the convex curve is replaced by a convex surface, usually by a sphere. One may also speak of a cone inscribed in a sphere, a sphere inscribed in a cone, etc. (Fig. c).
References
| [1] | D.I. Perepelkin, "A course of elementary geometry" , 1–2 , Moscow-Leningrad (1948–1949) (In Russian) |
Comments
References
| [a1] | M. Berger, "Geometry" , 1–2 , Springer (1987) (Translated from French) |
| [a2] | H.S.M. Coxeter, "Introduction to geometry" , Wiley (1961) pp. 11; 258 |
| [a3] | H.S.M. Coxeter, "Unvergängliche Geometrie" , Birkhäuser (1981) pp. 25; 313 |
Inscribed and circumscribed figures. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Inscribed_and_circumscribed_figures&oldid=12164