Stiefel manifold
(real)
The manifold  of orthonormal
of orthonormal  -frames in an
-frames in an  -dimensional Euclidean space. In a similar way one defines a complex Stiefel manifold
-dimensional Euclidean space. In a similar way one defines a complex Stiefel manifold  and a quaternion Stiefel manifold
and a quaternion Stiefel manifold  . Stiefel manifolds are compact real-analytic manifolds, and also homogeneous spaces of the classical compact groups
. Stiefel manifolds are compact real-analytic manifolds, and also homogeneous spaces of the classical compact groups  ,
,  and
and  , respectively. In particular,
, respectively. In particular,  ,
,  ,
,  are the spheres, the Stiefel manifold
are the spheres, the Stiefel manifold  is the manifold of unit vectors tangent to
is the manifold of unit vectors tangent to  , the Stiefel manifolds
, the Stiefel manifolds  ,
,  ,
,  are identified with the groups
are identified with the groups  ,
,  ,
,  , and
, and  — with the group
— with the group 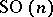 . Sometimes non-compact Stiefel manifolds, consisting of all possible
. Sometimes non-compact Stiefel manifolds, consisting of all possible  -frames in
-frames in  ,
, 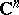 or
or  , are considered.
, are considered.
These manifolds were introduced by E. Stiefel [1] in connection with systems of linearly independent vector fields on smooth manifolds. First started in [1], studies on the topology of Stiefel manifolds led later to the complete calculation of their cohomology rings (see [2], [3]). In particular,
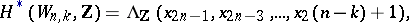 |
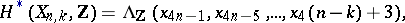 |
 is a commutative algebra with generators
is a commutative algebra with generators  and relations
and relations
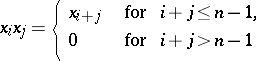 |
(everywhere above,  denotes an element of order
denotes an element of order  ). Real, complex and quaternion Stiefel manifolds are aspherical in dimensions not exceeding
). Real, complex and quaternion Stiefel manifolds are aspherical in dimensions not exceeding  ,
, 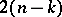 and
and  , respectively. Moreover,
, respectively. Moreover,
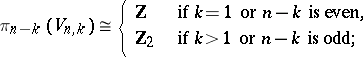 |
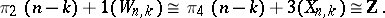 |
The computation of other homotopy groups of Stiefel manifolds is discussed in [5].
References
| [1] | E. Stiefel, "Richtungsfelder und Fernparallelismus in  -dimensionalen Mannigfaltigkeiten" Comm. Math. Helv. , 8 : 4 (1935–1936) pp. 305–353 -dimensionalen Mannigfaltigkeiten" Comm. Math. Helv. , 8 : 4 (1935–1936) pp. 305–353 |
| [2] | A. Borel, , Fibre spaces and their applications , Moscow (1958) pp. 163–246 (In Russian; translated from French) |
| [3] | N.E. Steenrod, D.B.A. Epstein, "Cohomology operations" , Princeton Univ. Press (1962) |
| [4] | V.A. Rokhlin, D.B. Fuks, "Beginner's course in topology. Geometric chapters" , Springer (1984) (Translated from Russian) |
| [5] | Itogi Nauk. Algebra. Topol. Geom. (1971) pp. 71–122 |
Comments
For homotopy groups of Stiefel manifolds see also .
Another (and better) frequently used notation for the Stiefel manifolds  ,
,  and
and 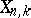 is
is  ,
,  ,
,  , generalizing to
, generalizing to 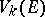 where
where  is an appropriate vector space.
is an appropriate vector space.
As homogeneous spaces these Stiefel manifolds are equal to, respectively,
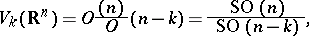 |
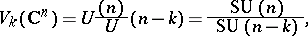 |
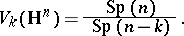 |
The natural quotient mapping  , etc., assigns to an orthogonal, etc., matrix the
, etc., assigns to an orthogonal, etc., matrix the  -frame consisting of its first
-frame consisting of its first  columns.
columns.
There are canonical mappings from the Stiefel manifolds to the Grassmann manifolds (cf. Grassmann manifold):
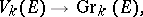 |
which assign to a 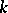 -frame the
-frame the 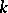 -dimensional subspace spanned by that frame. This exhibits the Grassmann manifolds as homogeneous spaces:
-dimensional subspace spanned by that frame. This exhibits the Grassmann manifolds as homogeneous spaces:
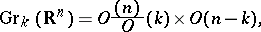 |
etc.
Given an  -dimensional (real, complex, quaternionic) vector bundle
-dimensional (real, complex, quaternionic) vector bundle 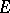 over a space
over a space  , the associated Stiefel bundles
, the associated Stiefel bundles  have the fibres
have the fibres 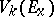 over
over  , where
, where  is the fibre of
is the fibre of 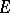 over
over  . Similarly one has the Grassmann bundle
. Similarly one has the Grassmann bundle  , whose fibre over
, whose fibre over 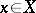 is the Grassmann manifold
is the Grassmann manifold 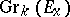 .
.
References
| [a1] | D. Husemoller, "Fibre bundles" , McGraw-Hill (1966) |
| [a2] | J. Dieudonné, "A history of algebraic and differential topology 1900–1960" , Birkhäuser (1989) |
| [a3a] | G.F. Paechter, "The groups 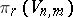 " Quarterly J. Math. , 7 (1956) pp. 249–268 " Quarterly J. Math. , 7 (1956) pp. 249–268 |
| [a3b] | G.F. Paechter, "The groups 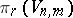 " Quarterly J. Math. , 9 (1958) pp. 8–27 " Quarterly J. Math. , 9 (1958) pp. 8–27 |
| [a3c] | G.F. Paechter, "The groups 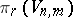 " Quarterly J. Math. , 10 (1959) pp. 17–37; 241–260 " Quarterly J. Math. , 10 (1959) pp. 17–37; 241–260 |
| [a3d] | G.F. Paechter, "The groups 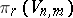 " Quarterly J. Math. , 11 (1960) pp. 1–16 " Quarterly J. Math. , 11 (1960) pp. 1–16 |
| [a4] | M.W. Hirsch, "Differential topology" , Springer (1976) pp. 4, 78 |
| [a5] | J.W. Milnor, J.D. Stasheff, "Characteristic classes" , Princeton Univ. Press (1974) |
Stiefel manifold. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stiefel_manifold&oldid=49446