Skew-symmetric bilinear form

anti-symmetric bilinear form

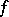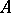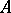A bilinear form on a unitary -module (where is a commutative ring with an identity) such that

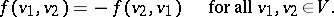The structure of any skew-symmetric bilinear form 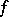on a finite-dimensional vector space 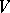over a field of characteristic 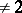is uniquely determined by its Witt index 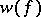(see Witt theorem; Witt decomposition). Namely: 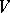is the orthogonal (with respect to 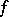) direct sum of the kernel 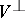of 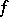and a subspace of dimension 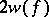, the restriction of 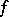to which is a standard form. Two skew-symmetric bilinear forms on 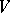are isometric if and only if their Witt indices are equal. In particular, a non-degenerate skew-symmetric bilinear form is standard, and in that case the dimension of 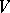is even.

For any skew-symmetric bilinear form 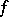on there exists a basis relative to which the matrix of 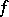is of the form

(*)

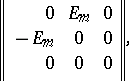where 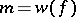and 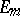is the identity matrix of order 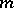. The matrix of a skew-symmetric bilinear form relative to any basis is skew-symmetric. Therefore, the above properties of skew-symmetric bilinear forms can be formulated as follows: For any skew-symmetric matrix 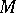over a field of characteristic 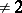there exists a non-singular matrix 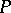such that 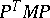is of the form (*). In particular, the rank of 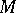is even, and the determinant of a skew-symmetric matrix of odd order is 0.

The above assertions remain valid for a field of characteristic 2, provided one replaces the skew-symmetry condition for the form 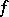by the condition that the form be alternating: 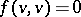for any 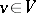(for fields of characteristic 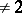the two conditions are equivalent).

These results can be generalized to the case where 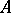is a commutative principal ideal ring, 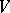is a free 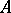-module of finite dimension and 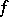is an alternating bilinear form on 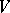. To be precise: Under these assumptions there exists a basis of the module 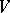and a non-negative integer 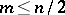such that

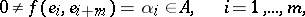and 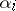divides 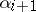for 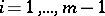; otherwise 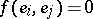. The ideals 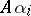are uniquely determined by these conditions, and the module 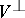is generated by .

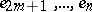The determinant of an alternating matrix of odd order equals 0 for any commutative ring 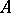with an identity. In case the order of the alternating matrix 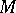over 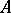is even, the element 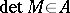is a square in 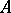(see Pfaffian).

References

[1]	N. Bourbaki, "Algèbre" , Eléments de mathématiques , Hermann (1970) pp. Chapt. II. Algèbre linéaire
[2]	S. Lang, "Algebra" , Addison-Wesley (1984)
[3]	E. Artin, "Geometric algebra" , Interscience (1957)

Comments

The kernel of a skew-symmetric bilinear form is the left kernel of the corresponding bilinear mapping, which is equal to the right kernel by skew symmetry.

References

[a1]	J. Milnor, D. Husemoller, "Symmetric bilinear forms" , Springer (1973)