User:Maximilian Janisch/latexlist/latex/NoNroff/46

List

1. 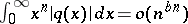 ; $\int _ { 0 } ^ { \infty } x ^ { n } | q ( x ) | d x = o ( n ^ { b n } )$ ; confidence 0.714

2. 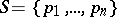 ; $S = \{ p _ { 1 } , \dots , p _ { n } \}$ ; confidence 0.714

3. 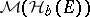 ; $\mathcal{M} ( \mathcal{H} _ { b } ( E ) )$ ; confidence 0.714

4. 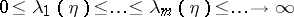 ; $0 \leq \lambda _ { 1 } ( \eta ) \leq \ldots \leq \lambda _ { m } ( \eta ) \leq \ldots \rightarrow \infty$ ; confidence 0.714

5. 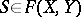 ; $S \in F ( X , Y )$ ; confidence 0.714

6. 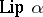 ; $\operatorname { Lip } \alpha$ ; confidence 0.714

7. 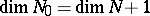 ; $\operatorname { dim } N _ { 0 } = \operatorname { dim } N + 1$ ; confidence 0.714

8. 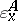 ; $\varepsilon _ { X } ^ { A }$ ; confidence 0.714

9. 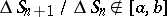 ; $\Delta S _ { n + 1 } / \Delta S _ { n } \notin [ a , b ]$ ; confidence 0.713

10. 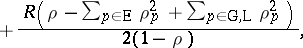 ; $+ \frac { R \left( \rho - \sum _ { p \in E } \rho _ { p } ^ { 2 } + \sum _ { p \in \text{G,L} } \rho _ { p } ^ { 2 } \right) } { 2 ( 1 - \rho ) },$ ; confidence 0.713

11. 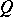 ; $Q$ ; confidence 0.713

12. 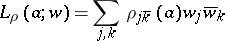 ; $L _ { \rho } ( a ; w ) = \sum _ { j , k } \rho _ { j \overline { k } } ( a ) w _ { j } \overline { w } _ { k }$ ; confidence 0.713

13. 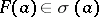 ; $F ( a ) \in \sigma ( a )$ ; confidence 0.713

14. 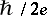 ; $\hbar \nmid 2 e$ ; confidence 0.713

15.  ; $\frac { 1 } { 12 \pi ^ { 2 } } \omega _{\text{WP}}.$ ; confidence 0.713

16. 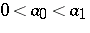 ; $0 < a _ { 0 } < a _ { 1 }$ ; confidence 0.713

17. 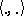 ; $\langle \, .\, ,\, . \, \rangle$ ; confidence 0.713

18. 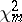 ; $\chi ^ { 2 }_{m}$ ; confidence 0.713

19. 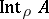 ; $\operatorname { Int } _ { \rho } A$ ; confidence 0.713

20. 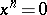 ; $x ^ { n } = 0$ ; confidence 0.713

21. 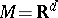 ; $M = \mathbf{R} ^ { d }$ ; confidence 0.713

22. 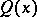 ; $Q ( x )$ ; confidence 0.713

23.  ; $\square _ { A } ^ { A } \mathcal{C}$ ; confidence 0.713

24. 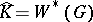 ; $\hat { K } = W ^ { * } ( G )$ ; confidence 0.713

25. 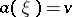 ; $a ( \xi ) = v$ ; confidence 0.713

26.  ; $am \otimes m + m _ { 1 } B _ { 1 } + \ldots + m _ { d } B _ { d } + C$ ; confidence 0.713

27. 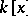 ; $k [ x ]$ ; confidence 0.713

28. 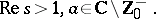 ; $\operatorname { Re } s > 1 , a \in \mathbf{C} \backslash \mathbf{Z} ^{ - } _ { 0 }.$ ; confidence 0.713

29. 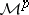 ; $\mathcal{M} ^ { p }$ ; confidence 0.712

30. 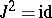 ; $J ^ { 2 } = \operatorname{id}$ ; confidence 0.712

31. 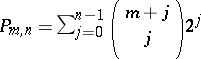 ; $P _ { m , n } = \sum _ { j = 0 } ^ { n - 1 } \left( \begin{array} { c } { m + j } \\ { j } \end{array} \right) 2 ^ { j }$ ; confidence 0.712

32. 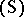 ; $( \operatorname{S} )$ ; confidence 0.712

33. 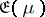 ; $\mathfrak{E} ( \mu )$ ; confidence 0.712

34. 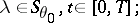 ; $\lambda \in S _ { \theta _ { 0 } } , t \in [ 0 , T ];$ ; confidence 0.712

35. 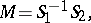 ; $M = S _ { 1 } ^ { - 1 } S _ { 2 },$ ; confidence 0.712

36. 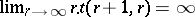 ; $\operatorname { lim } _ { r \rightarrow \infty } r \cdot t ( r + 1 , r ) = \infty$ ; confidence 0.712

37. 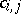 ; $c_{i , j}$ ; confidence 0.712

38.  ; $b _ { 3 }$ ; confidence 0.712

39. 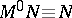 ; $M ^ { 0 } N \equiv N$ ; confidence 0.712

40. 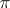 ; $\pi$ ; confidence 0.712

41. 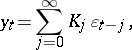 ; $y _ { t } = \sum _ { j = 0 } ^ { \infty } K _ { j } \varepsilon _ { t - j },$ ; confidence 0.712

42. 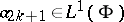 ; $a _ { 2 k + 1 } \in L ^ { 1 } ( \Phi )$ ; confidence 0.712

43. 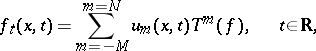 ; $f _ { t } ( x , t ) = \sum _ { m = - M } ^ { m = N } u _ { m } ( x , t ) T ^ { m } ( f ) , \quad t \in \mathbf{R},$ ; confidence 0.712

44. 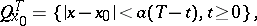 ; $Q _ { x _ { 0 } } ^ { T } = \{ | x - x _ { 0 } | < a ( T - t ) , t \geq 0 \},$ ; confidence 0.712

45. 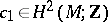 ; $c _ { 1 } \in H ^ { 2 } ( M ; \mathbf{Z} )$ ; confidence 0.712

46. 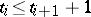 ; $t _ { i } \leq t_{i + 1} + 1$ ; confidence 0.712

47. 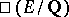 ; $\square ( E / \mathbf{Q} )$ ; confidence 0.712

48. 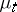 ; $\mu _ { t }$ ; confidence 0.712

49.  ; $( M , g ) = ( \mathbf{R} ^ { 2 } \backslash \{ 0 \} , 2 / ( u ^ { 2 } + v ^ { 2 } ) d u d v )$ ; confidence 0.712

50. 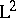 ; $\operatorname{L} ^ { 2 }$ ; confidence 0.712

51. 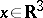 ; $x \in \mathbf{R} ^ { 3 }$ ; confidence 0.712

52. 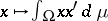 ; $x \mapsto \int _ { \Omega } x x ^ { \prime } d \mu$ ; confidence 0.712

53. 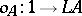 ; $o _ { A } : 1 \rightarrow L A$ ; confidence 0.712

54. 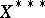 ; $X ^ { * * * }$ ; confidence 0.711

55. 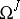 ; $\Omega ^ { J }$ ; confidence 0.711

56. 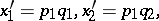 ; $x _ { 1 } ^ { \prime } = p _ { 1 } q _ { 1 } ,\, x _ { 2 } ^ { \prime } = p _ { 1 } q _ { 2 },$ ; confidence 0.711

57. 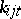 ; $k_{i j t}$ ; confidence 0.711

58. 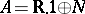 ; $A = \mathbf{R} .1 \oplus N$ ; confidence 0.711

59. 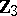 ; $\mathbf{Z}_{3}$ ; confidence 0.711

60.  ; $L : = P _ { 0 } \frac { d } { d x } + P _ { 1 } = \left( \begin{array} { c c } { - i } & { 0 } \\ { 0 } & { i } \end{array} \right) \frac { d } { d x } + \left( \begin{array} { c c } { 0 } & { q } \\ { r } & { 0 } \end{array} \right),$ ; confidence 0.711

61. 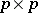 ; $p \times p$ ; confidence 0.711

62. 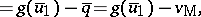 ; $= g ( \overline { u } _ { 1 } ) - \overline { q } = g ( \overline { u } _ { 1 } ) - v _ { \text{M} },$ ; confidence 0.711

63.  ; $A _ { i } \cap ( - A _ { i } ) = \emptyset$ ; confidence 0.711

64. 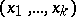 ; $( x _ { 1 } , \dots , x _ { k } )$ ; confidence 0.711

65. 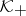 ; $\mathcal{K} _ { + }$ ; confidence 0.711

66. 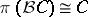 ; $\pi ( \mathcal{B} C ) \cong C$ ; confidence 0.711

67. 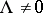 ; $\Lambda \neq 0$ ; confidence 0.711

68. 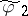 ; $\tilde { \varphi }_{2}$ ; confidence 0.711

69. 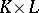 ; $K \times L$ ; confidence 0.711

70. 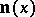 ; $\mathbf{n} ( x )$ ; confidence 0.711

71. 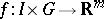 ; $f : I \times G \rightarrow \mathbf{R} ^ { m }$ ; confidence 0.711

72. 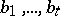 ; $b _ { 1 } , \dots , b _ { t }$ ; confidence 0.710

73.  ; $| a _ { n } | \rightarrow \infty$ ; confidence 0.710

74.  ; $L | F$ ; confidence 0.710

75. 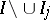 ; $I \backslash \cup I_{j}$ ; confidence 0.710

76. 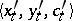 ; $\langle x _ { t } ^ { \prime } , y _ { t } ^ { \prime } , c _ { t } ^ { \prime } \rangle$ ; confidence 0.710

77. 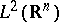 ; $L ^ { 2 } ( \mathbf{R} ^ { n } )$ ; confidence 0.710

78. 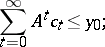 ; $\sum _ { t = 0 } ^ { \infty } A ^ { t } c_{ t} \leq y_0;$ ; confidence 0.710

79. 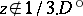 ; $z \notin 1 / 3 . D ^ { \circ }$ ; confidence 0.710

80. 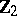 ; $\mathbf{Z}_{2}$ ; confidence 0.710

81. 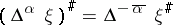 ; $( \Delta ^ { \alpha } \xi ) ^ { \# } = \Delta ^ { - \overline { \alpha } } \xi ^ { \# }$ ; confidence 0.710

82. 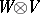 ; $W \otimes V$ ; confidence 0.710

83. 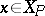 ; $x \in X _ { P }$ ; confidence 0.710

84. 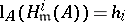 ; $\operatorname{l} _ { A } ( H _ { \text{m} } ^ { i } ( A ) ) = h _ { i }$ ; confidence 0.710

85. 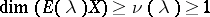 ; $\operatorname { dim } ( E ( \lambda ) X ) \geq \nu ( \lambda ) \geq 1$ ; confidence 0.710

86. 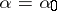 ; $\alpha = \alpha _ { 0 }$ ; confidence 0.709

87. 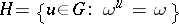 ; $H = \{ u \in G : \omega ^ { u } = \omega \}$ ; confidence 0.709

88. 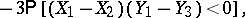 ; $- 3 \mathsf{P} [ ( X _ { 1 } - X _ { 2 } ) ( Y _ { 1 } - Y _ { 3 } ) < 0 ],$ ; confidence 0.709

89. 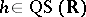 ; $h \in \operatorname {QS} ( \mathbf{R} )$ ; confidence 0.709

90. 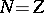 ; $N = Z$ ; confidence 0.709

91. 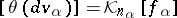 ; $[ \theta ( d v _ { \alpha } ) ] = \mathcal{K} _ { n _ { \alpha } } [ f _ { \alpha } ]$ ; confidence 0.709

92. 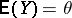 ; $\mathsf{E} ( Y ) = \theta$ ; confidence 0.709

93.  ; $p : ( X , * ) \rightarrow ( * , * )$ ; confidence 0.709

94. 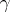 ; $\gamma$ ; confidence 0.709

95. 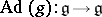 ; $\operatorname {Ad}( g ) : \mathfrak { g } \rightarrow \mathfrak { g }$ ; confidence 0.709

96. 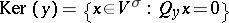 ; $\operatorname { Ker } ( y ) = \{ x \in V ^ { \sigma } : Q _ { y } x = 0 \}$ ; confidence 0.709

97. 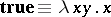 ; $\mathbf{true}\equiv \lambda x y \cdot x$ ; confidence 0.709

98. 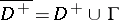 ; $\overline { D ^ { + } } = D ^ { + } \cup \Gamma$ ; confidence 0.709

99. 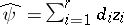 ; $\hat { \psi } = \sum _ { i = 1 } ^ { r } d _ { i } z _ { i }$ ; confidence 0.709

100. 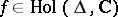 ; $f \in \operatorname { Hol } ( \Delta , \mathbf{C} )$ ; confidence 0.709

101.  ; $w , g ( w ) , g ^ { 2 } ( w ), \dots$ ; confidence 0.709

102. 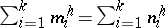 ; $\sum _ { i = 1 } ^ { k } m _ { i } ^ { h } = \sum _ { i = 1 } ^ { k } n _ { i } ^ { h }$ ; confidence 0.709

103. 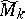 ; $\tilde { M } _ { k }$ ; confidence 0.709

104. 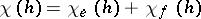 ; $\chi ( h ) = \chi _ { e } ( h ) + \chi_{f }( h )$ ; confidence 0.709

105. 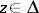 ; $z \in \Delta$ ; confidence 0.709

106. 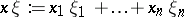 ; $x \xi : = x _ { 1 } \xi _ { 1 } + \ldots + x _ { n } \xi _ { n }$ ; confidence 0.708

107.  ; $t = b$ ; confidence 0.708

108. 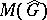 ; $M ( \hat { G } )$ ; confidence 0.708

109.  ; $P _ { 0 } | 0 \rangle = | 0 \rangle$ ; confidence 0.708

110. 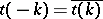 ; $t ( - k ) = \overline { t ( k ) }$ ; confidence 0.708

111.  ; $\mathbf{F} _ { 2 }$ ; confidence 0.708

112. 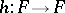 ; $h : F \rightarrow F$ ; confidence 0.708

113.  ; $A \mathbf{x} \in \tilde { B }$ ; confidence 0.708

114. 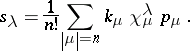 ; $s _ { \lambda } = \frac { 1 } { n ! } \sum _ { | \mu | = n } k _ { \mu } \chi _ { \mu } ^ { \lambda } p _ { \mu }.$ ; confidence 0.708

115.  ; $x _ { j t }$ ; confidence 0.708

116. 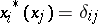 ; $x _ { i } ^ { * } ( x _ { j } ) = \delta _ { i j }$ ; confidence 0.708

117. 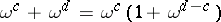 ; $\omega ^ { c } + \omega ^ { d } = \omega ^ { c } ( 1 + \omega ^ { d - c } )$ ; confidence 0.708

118. 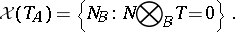 ; $\chi ( T _ { A } ) = \left\{ N _ { B } : N \bigotimes _ { B } T = 0 \right\}.$ ; confidence 0.708

119. 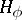 ; $H _ { \phi }$ ; confidence 0.708

120.  ; $\sum _ { j = n - k } ^ { n + 1 } b _ { n , j } P _ { j } ( x ) = \sum _ { j = n - k } ^ { n + 1 } \beta _ { n + 1 , j } Q _ { j } ( x ).$ ; confidence 0.708

121. 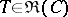 ; $T \in \Re ( C )$ ; confidence 0.707

122. 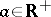 ; $a \in \mathbf{R} ^ { + }$ ; confidence 0.707

123. 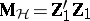 ; $\mathbf{M} _ { \mathcal{H} } = \mathbf{Z} _ { 1 } ^ { \prime }\mathbf{ Z} _ { 1 }$ ; confidence 0.707

124. 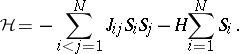 ; $\mathcal{H} = - \sum _ { i < j = 1 } ^ { N } J _ { i j } S _ { i } S _ { j } - H \sum _ { i = 1 } ^ { N } S _ { i }.$ ; confidence 0.707

125. 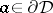 ; $a \in \partial \mathcal{D}$ ; confidence 0.707

126. 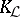 ; $K _ { \mathcal{L} }$ ; confidence 0.707

127. 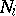 ; $N_{i}$ ; confidence 0.707

128. 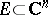 ; $E \subset \mathbf{C} ^ { n }$ ; confidence 0.707

129. 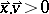 ; $\overset{\rightharpoonup}{x} . \overset{\rightharpoonup}{ v } > 0$ ; confidence 0.707

130. 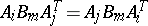 ; $A _ { i } B _ { m } A _ { j } ^ { T } = A _ { j } B _ { m } A _ { i } ^ { T }$ ; confidence 0.707

131. 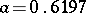 ; $a = 0.6197$ ; confidence 0.707

132. 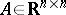 ; $A \in \mathbf{R} ^ { n \times n }$ ; confidence 0.707

133. 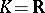 ; $K = \mathbf{R}$ ; confidence 0.707

134. 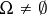 ; $\Omega \neq \emptyset$ ; confidence 0.707

135.  ; $a ( x , \alpha , p ) : = \frac { 1 } { ( 2 \pi ) ^ { n } } \int _ { 0 } ^ { \infty } t ^ { n - 1 } e ^ { - i t p } b ( x , t , \alpha ) d t,$ ; confidence 0.706

136.  ; $\Omega \subset \mathbf{R} ^ { n }$ ; confidence 0.706

137. 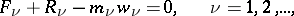 ; $F _ { \nu } + R _ { \nu } - m _ { \nu } w _ { \nu } = 0 , \quad \nu = 1,2 , \dots ,$ ; confidence 0.706

138. 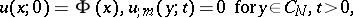 ; $u ( x ; 0 ) = \Phi ( x ) , u _ { ; m } ( y ; t ) = 0 \text { for } y \in C _ { N } , t > 0,$ ; confidence 0.706

139. 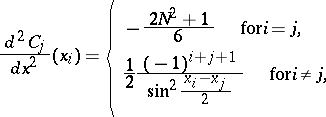 ; $\frac { d ^ { 2 } C _ { j } } { d x ^ { 2 } } ( x _ { i } ) = \left\{ \begin{array} { l l } { - \frac { 2 N ^ { 2 } + 1 } { 6 } } & { \text { for } i = j, } \\ { \frac { 1 } { 2 } \frac { ( - 1 ) ^ { i + j + 1 } } { \operatorname { sin } ^ { 2 } \frac { x _ { i } - x _ { j } } { 2 } } } & { \text { for } i \neq j, } \end{array} \right.$ ; confidence 0.706

140. 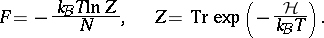 ; $F = - \frac { k _ { B } T \operatorname { ln } Z } { N } , \quad Z = \operatorname { Tr } \operatorname { exp } \left( - \frac { \mathcal{H} } { k _ { B } T } \right).$ ; confidence 0.706

141. 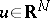 ; $u \in \mathbf{R} ^ { N }$ ; confidence 0.706

142. 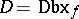 ; $D = \operatorname{Dbx} _ { f }$ ; confidence 0.706

143. 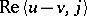 ; $\operatorname { Re } \langle u - v , j \rangle$ ; confidence 0.706

144. 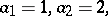 ; $a _ { 1 } = 1 , a _ { 2 } = 2$ ; confidence 0.706

145. 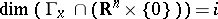 ; $\operatorname { dim } ( \Gamma _ { X } \cap ( \mathbf{R} ^ { n } \times \{ 0 \} ) ) = i$ ; confidence 0.706

146. 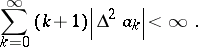 ; $\sum _ { k = 0 } ^ { \infty } ( k + 1 ) \left| \Delta ^ { 2 } \alpha _ { k } \right| < \infty.$ ; confidence 0.706

147. 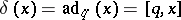 ; $\delta ( x ) = \operatorname { ad } _ { q } ( x ) = [ q , x ]$ ; confidence 0.706

148. 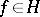 ; $f \in H$ ; confidence 0.705

149. 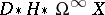 ; $D _{*} H _{*} \Omega ^ { \infty } X$ ; confidence 0.705

150.  ; $\mathsf{E} [ T _ { p } ] = \mathsf{E} [ W _ { p } ] + b _ { p }$ ; confidence 0.705

151. 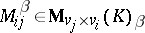 ; $M _ { i j } ^ { \beta } \in \mathbf{M} _ { v _ { j } \times v _ { i } } ( K ) _ { \beta }$ ; confidence 0.705

152. 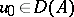 ; $u _ { 0 } \in D ( A )$ ; confidence 0.705

153. 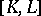 ; $[ K , L ]$ ; confidence 0.705

154. 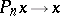 ; $P _ { n } x \rightarrow x$ ; confidence 0.705

155. 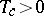 ; $T _ { c } > 0$ ; confidence 0.705

156. 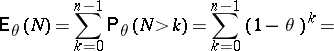 ; $\mathsf{E} _ { \theta } ( N ) = \sum _ { k = 0 } ^ { n - 1 } \mathsf{P} _ { \theta } ( N > k ) = \sum _ { k = 0 } ^ { n - 1 } ( 1 - \theta ) ^ { k } =$ ; confidence 0.705

157. 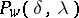 ; $P _ { W } ( \delta , \lambda )$ ; confidence 0.705

158. 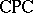 ; $\operatorname{CPC}$ ; confidence 0.705

159. 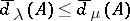 ; $\overline { d } _ { \lambda } ( A ) \leq \overline { d } _ { \mu } ( A )$ ; confidence 0.705

160.  ; $X \in \mathcal{F}$ ; confidence 0.705

161. 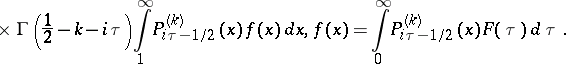 ; $\times \Gamma \left( \frac { 1 } { 2 } - k - i \tau \right) \int _ { 1 } ^ { \infty } P _ { i \tau - 1/2 } ^ { ( k ) } ( x ) f ( x ) d x , f ( x ) = \int _ { 0 } ^ { \infty } P _ { i \tau -1/2} ^ { ( k ) } ( x ) F ( \tau ) d \tau.$ ; confidence 0.705

162. 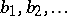 ; $b _ { 1 } , b _ { 2 } , \dots$ ; confidence 0.705

163. 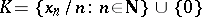 ; $K = \{ x _ { n } / n : n \in \mathbf{N} \} \cup \{ 0 \}$ ; confidence 0.705

164.  ; $J ^ { \prime } \mapsto M ^ { \prime t } J ^ { \prime } M ^ { \prime }$ ; confidence 0.705

165. 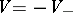 ; $V = - V _ { - }$ ; confidence 0.705

166. 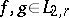 ; $f , g \in L _ { 2 , r }$ ; confidence 0.705

167. 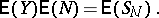 ; $\mathsf{E} ( Y ) \mathsf{E} ( N ) = \mathsf{E} ( S _ { N } ).$ ; confidence 0.705

168. 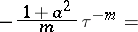 ; $- \frac { 1 + a ^ { 2 } } { m } \tau ^ { - m } =$ ; confidence 0.705

169. 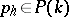 ; $p _ { h } \in P ( k )$ ; confidence 0.705

170. 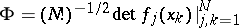 ; $\Phi = ( N ! ) ^ { - 1 / 2 } \operatorname { det } f _ { j } ( x _ { k } ) | _ { j , k = 1 } ^ { N }$ ; confidence 0.704

171. 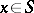 ; $x \in S$ ; confidence 0.704

172. 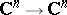 ; $\mathbf{C} ^ { n } \rightarrow \mathbf{C} ^ { n }$ ; confidence 0.704

173. 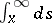 ; $\int _ { X } ^ { \infty } d s$ ; confidence 0.704

174. 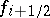 ; $f _ { i + 1 / 2 }$ ; confidence 0.704

175. 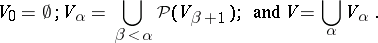 ; $V _ { 0 } = \emptyset ; V _ { \alpha } = \bigcup _ { \beta < \alpha } \mathcal{P} ( V _ { \beta + 1 } ) ; \text { and } V = \bigcup _ { \alpha } V _ { \alpha }.$ ; confidence 0.704

176. 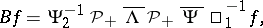 ; $B f = \Psi _ { 2 } ^ { - 1 } \mathcal{P} _ { + } \overline { \Lambda } \mathcal{P} _ { + } \overline { \Psi } \square ^ { - 1 }_{1} f,$ ; confidence 0.704

177. 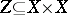 ; $Z \subseteq X \times X$ ; confidence 0.704

178. 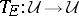 ; $T _ { E } : \mathcal{U} \rightarrow \mathcal{U} $ ; confidence 0.704

179. 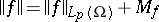 ; $\| f \| = \| f \| _ { L _ { p } ( \Omega ) } + M _ { f }$ ; confidence 0.704

180. 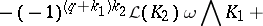 ; $- ( - 1 ) ^ { ( q + k _ { 1 } ) k _ { 2 } } \mathcal{L} ( K _ { 2 } ) \omega \bigwedge K _ { 1 } +$ ; confidence 0.704

181. 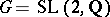 ; $G = \operatorname{SL} ( 2 , \mathbf{Q} )$ ; confidence 0.704

182. 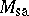 ; $M _ { \operatorname{sa} }$ ; confidence 0.704

183. 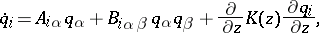 ; $\dot { q } _ { i } = A _ { i \alpha } q _ { \alpha } + B _ { i \alpha \beta } q _ { \alpha } q _ { \beta } + \frac { \partial } { \partial z } K ( z ) \frac { \partial q _ { i } } { \partial z },$ ; confidence 0.704

184. 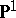 ; $\mathbf{P}^{1}$ ; confidence 0.704

185. 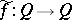 ; $\tilde { f } : Q \rightarrow Q$ ; confidence 0.704

186. 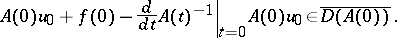 ; $A ( 0 ) u _ { 0 } + f ( 0 ) - \frac { d } { d t } A ( t ) ^ { - 1 } | _ { t = 0 } A ( 0 ) u _ { 0 } \in \overline { D ( A ( 0 ) ) }.$ ; confidence 0.704

187. 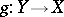 ; $g : Y \rightarrow X$ ; confidence 0.703

188.  ; $\mathcal{P} ( \square ^ { n } E ) \rightarrow \mathcal{P} ( \square ^ { n } E ^ { * * } )$ ; confidence 0.703

189. 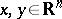 ; $x , y \in \mathbf{R} ^ { n }$ ; confidence 0.703

190. 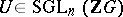 ; $U \in \operatorname{SGL} _ { n } ( \mathbf{Z} G )$ ; confidence 0.703

191. 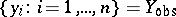 ; $\{ y _ { i } : i = 1 , \dots , n \} = Y _ { \operatorname{obs} }$ ; confidence 0.703

192. 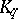 ; $K _ { q }$ ; confidence 0.703

193. 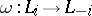 ; $\omega : L _ { i } \rightarrow L _ { - i }$ ; confidence 0.703

194. 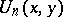 ; $U _ { n } ( x , y )$ ; confidence 0.703

195.  ; $| x | \rightarrow \infty$ ; confidence 0.702

196. 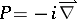 ; $P = - i \overset{\rightharpoonup}{ \nabla }$ ; confidence 0.702

197. 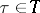 ; $\tau \in T$ ; confidence 0.702

198. 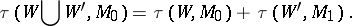 ; $\tau ( W \bigcup W ^ { \prime } , M _ { 0 } ) = \tau ( W , M _ { 0 } ) + \tau ( W ^ { \prime } , M _ { 1 } ).$ ; confidence 0.702

199. 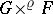 ; $G \times^{\varrho} F$ ; confidence 0.702

200. 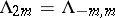 ; $\Lambda _ { 2 m } = \Lambda - m , m$ ; confidence 0.702

201. 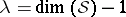 ; $\lambda = \operatorname { dim } ( \mathcal{S} ) - 1$ ; confidence 0.702

202. 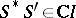 ; $S ^ { * } S ^ { \prime } \in \mathbf{C}I$ ; confidence 0.702

203. 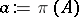 ; $a : = \pi ( A )$ ; confidence 0.702

204. 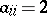 ; $\alpha _ { i j } = 2$ ; confidence 0.702

205. 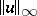 ; $\| u \|_{\infty}$ ; confidence 0.702

206.  ; $\hat { f }^{\prime}$ ; confidence 0.702

207. 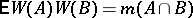 ; $\mathsf{E} W ( A ) W ( B ) = m ( A \cap B )$ ; confidence 0.702

208.  ; $\operatorname { map } _ { * } ( X \wedge S ^ { 1 } , Y ) \approx \operatorname { map } _ { * } ( X , \operatorname { map } _ { * } ( S ^ { 1 } , Y ) )$ ; confidence 0.702

209. 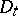 ; $D _ { t }$ ; confidence 0.702

210. 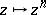 ; $z \mapsto z ^ { n }$ ; confidence 0.701

211.  ; $r = s$ ; confidence 0.701

212. 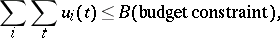 ; $\sum _ { i } \sum _ { t } u _ { i } ( t ) \leq B (\text{budget constraint}),$ ; confidence 0.701

213. 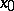 ; $x _ { 0 }$ ; confidence 0.701

214. 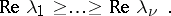 ; $\operatorname { Re } \lambda _ { 1 } \geq \ldots \geq \operatorname { Re } \lambda _ { \nu }.$ ; confidence 0.701

215. 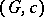 ; $( G , c )$ ; confidence 0.701

216.  ; $R _ { V }$ ; confidence 0.700

217. 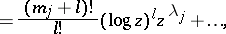 ; $= \frac { ( m _ { j } + l ) ! } { l ! } ( \operatorname { log } z ) ^ { l } z ^ { \lambda _ { j } } + \ldots,$ ; confidence 0.700

218. 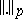 ; $\| . \| p$ ; confidence 0.700

219. 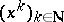 ; $( x ^ { k } ) _ { k \in \mathbf{N} }$ ; confidence 0.700

220.  ; $p ( x ) = \overline{0}$ ; confidence 0.700

221. 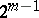 ; $2 ^ { m - 1 }$ ; confidence 0.700

222. 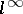 ; $l ^ { \infty }$ ; confidence 0.700

223. 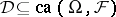 ; $\mathcal{D} \subseteq \operatorname{ ca} ( \Omega , \mathcal{F} )$ ; confidence 0.700

224. 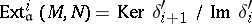 ; $\operatorname { Ext } _ { a } ^ { i } ( M , N ) = \operatorname { Ker } \delta _ { i + 1 } ^ { \prime } / \operatorname { Im } \delta _ { i } ^ { \prime }$ ; confidence 0.700

225. 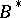 ; $B ^ { * }$ ; confidence 0.700

226. 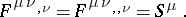 ; $F ^ { \mu \nu_{ , \nu} } = F ^ { \mu \nu_{ , , \nu}} = S ^ { \mu }.$ ; confidence 0.700

227. 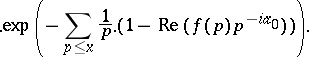 ; $.\operatorname { exp } \left( - \sum _ { p \leq x } \frac { 1 } { p } . ( 1 - \operatorname { Re } ( f ( p ) p ^ { - i \alpha _ { 0 } } ) ) \right).$ ; confidence 0.700

228.  ; $\tau \in H$ ; confidence 0.700

229.  ; $\mathbf{x} = \{ x _ { 1 } , \dots , x _ { l } \}$ ; confidence 0.700

230. 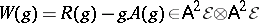 ; $W ( g ) = R ( g ) - g .A ( g ) \in \mathsf{A} ^ { 2 } \mathcal{E} \otimes \mathsf{A} ^ { 2 } \mathcal{E} $ ; confidence 0.700

231. 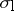 ; $\sigma_{\text{l}}$ ; confidence 0.700

232. 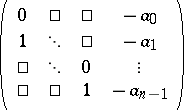 ; $\left( \begin{array} { c c c c } { 0 } & { \square } & { \square } & { - a _ { 0 } } \\ { 1 } & { \ddots } & { \square } & { - a _ { 1 } } \\ { \square } & { \ddots } & { 0 } & { \vdots } \\ { \square } & { \square } & { 1 } & { - a _ { n - 1 } } \end{array} \right)$ ; confidence 0.700

233. 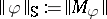 ; $\| \varphi \| _ { \text{S} } : = \| M_{ \varphi }\|$ ; confidence 0.700

234. 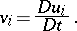 ; $v _ { i } = \frac { D u _ { i } } { D t }.$ ; confidence 0.700

235. 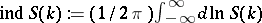 ; $\operatorname{ ind } S ( k ) : = ( 1 / 2 \pi ) \int _ { - \infty } ^ { \infty } d \operatorname { ln } S ( k )$ ; confidence 0.700

236. 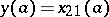 ; $y ( a ) = x _ { 21 } ( a )$ ; confidence 0.699

237. 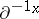 ; $\partial ^ { - 1_{x} }$ ; confidence 0.699

238. 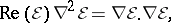 ; $\operatorname { Re } ( \mathcal{E} ) \nabla ^ { 2 } \mathcal{E} = \nabla \mathcal{E} . \nabla \mathcal{E},$ ; confidence 0.699

239. 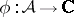 ; $\phi : \mathcal{A} \rightarrow \mathbf{C}$ ; confidence 0.699

240. 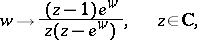 ; $w \rightarrow \frac { ( z - 1 ) e ^ { w } } { z ( z - e ^ { w } ) } , \quad z \in \mathbf{C},$ ; confidence 0.699

241. 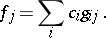 ; $f _ { j } = \sum _ { i } c _ { i } g _ {i j }.$ ; confidence 0.699

242.  ; $L : A \rightarrow \operatorname { Fun } _ { q } ( G ) \otimes A$ ; confidence 0.699

243. 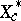 ; $X ^ { * }_{c}$ ; confidence 0.699

244. 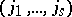 ; $( j _ { 1 } , \dots , j _ { s } )$ ; confidence 0.699

245. 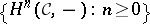 ; $\{ H ^ { n } ( \mathcal{C} , - ) : n \geq 0 \}$ ; confidence 0.699

246. 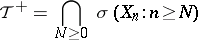 ; $\mathcal{T} ^ { + } = \bigcap _ { N \geq 0 } \sigma ( X _ { n } : n \geq N )$ ; confidence 0.699

247.  ; $A \mathbf{x} \leq \mathbf{b}$ ; confidence 0.699

248. 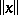 ; $\| x \|$ ; confidence 0.699

249. 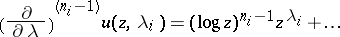 ; $\left( \frac { \partial } { \partial \lambda } \right) ^ { ( n _ { i } - 1 ) } u ( z , \lambda _ { i } ) = ( \operatorname { log } z ) ^ { n _ { i } - 1 } z ^ { \lambda _ { i } } +\dots$ ; confidence 0.699

250. 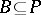 ; $B \subseteq P$ ; confidence 0.699

251.  ; $P _ { N } u = \sum _ { k = - N } ^ { N } a _ { k } e ^ { i k x }$ ; confidence 0.699

252. 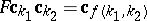 ; $F \mathbf{c} _ { k _ { 1 } } \mathbf{c} _ { k _ { 2 } } = \mathbf{c} _ { f ( k _ { 1 } , k _ { 2 } )}$ ; confidence 0.698

253. 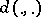 ; $d ( . , . )$ ; confidence 0.698

254. 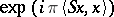 ; $\operatorname { exp } ( i \pi \langle S x , x \rangle )$ ; confidence 0.698

255. 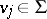 ; $v _ { j } \in \Sigma$ ; confidence 0.698

256. 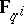 ; $\mathbf{F} _ { q ^ { i } }$ ; confidence 0.698

257. 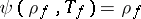 ; $\psi ( \rho _ { f } , T _ { f } ) = \rho _ { f }$ ; confidence 0.698

258. 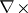 ; $\nabla \times$ ; confidence 0.698

259. 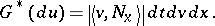 ; $G ^ { * } ( d u ) = | \langle v , N _ { x } \rangle | d t d v d x.$ ; confidence 0.698

260. 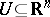 ; $U \subseteq \mathbf{R} ^ { n }$ ; confidence 0.698

261. 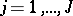 ; $j = 1 , \ldots , J$ ; confidence 0.698

262. 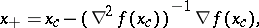 ; $x _ { + } = x _ { c } - ( \nabla ^ { 2 } f ( x _ { c } ) ) ^ { - 1 } \nabla f ( x _ { c } ),$ ; confidence 0.698

263.  ; $\chi _ { l } ^ { \prime } ( G ) \leq \Delta ( G ) + 1$ ; confidence 0.698

264. 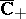 ; $\overline { \mathbf{C} } _ { + }$ ; confidence 0.698

265.  ; $D ( a , R )$ ; confidence 0.698

266. 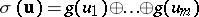 ; $\sigma ( \mathbf{u} ) = g ( u _ { 1 } ) \oplus \ldots \oplus g ( u _ { m } )$ ; confidence 0.698

267. 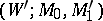 ; $( W ^ { \prime } ; M _ { 0 } , M _ { 1 } ^ { \prime } )$ ; confidence 0.698

268. 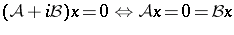 ; $( \mathcal{A} + i \mathcal{B} ) x = 0 \Leftrightarrow \mathcal{A} x = 0 = \mathcal{B} x$ ; confidence 0.698

269. 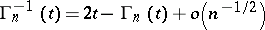 ; $\Gamma _ { n } ^ { - 1 } ( t ) = 2 t - \Gamma _ { n } ( t ) + o \left( n ^ { - 1 / 2 } \right)$ ; confidence 0.698

270. 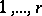 ; $1 , \ldots , r$ ; confidence 0.698

271. 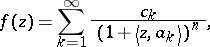 ; $f ( z ) = \sum _ { k = 1 } ^ { \infty } \frac { c _ { k } } { ( 1 + \langle z , \alpha _ { k } \rangle ) ^ { n } },$ ; confidence 0.698

272. 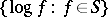 ; $\{ \operatorname { log } f : f \in S \}$ ; confidence 0.697

273.  ; $A _ { 1 } , \dots , A _ { k }$ ; confidence 0.697

274. 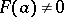 ; $F ( a ) \neq 0$ ; confidence 0.697

275. 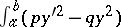 ; $\int _ { a } ^ { \phi } ( p y ^ { \prime 2 } - q y ^ { 2 } )$ ; confidence 0.697

276. 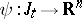 ; $\psi : J _ { t } \rightarrow \mathbf{R} ^ { n }$ ; confidence 0.697

277. 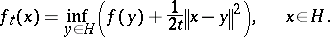 ; $f _ { t } ( x ) = \operatorname { inf } _ { y \in H } \left( f ( y ) + \frac { 1 } { 2 t } \| x - y \| ^ { 2 } \right) , \quad x \in H.$ ; confidence 0.697

278.  ; $b \in D$ ; confidence 0.697

279.  ; $\alpha : M \times G \rightarrow M$ ; confidence 0.697

280. 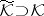 ; $\tilde { \mathcal{K} } \supset \mathcal{K}$ ; confidence 0.697

281. 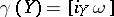 ; $\gamma ( Y ) = [ i \gamma \omega ]$ ; confidence 0.697

282. 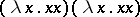 ; $( \lambda x . x x ) ( \lambda x . x x )$ ; confidence 0.697

283. 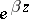 ; $e ^ { \beta z }$ ; confidence 0.697

284. 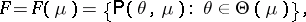 ; $F = F ( \mu ) = \{ \mathsf{P} ( \theta , \mu ) : \theta \in \Theta ( \mu ) \},$ ; confidence 0.697

285. 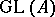 ; $\operatorname{GL} ( A )$ ; confidence 0.697

286. 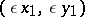 ; $( \epsilon x _ { 1 } , \epsilon y _ { 1 } )$ ; confidence 0.697

287. 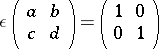 ; $\epsilon \left( \begin{array} { l l } { a } & { b } \\ { c } & { d } \end{array} \right) = \left( \begin{array} { l l } { 1 } & { 0 } \\ { 0 } & { 1 } \end{array} \right)$ ; confidence 0.697

288. 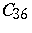 ; $C _ { 36 }$ ; confidence 0.697

289. 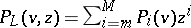 ; $P _ { L } ( v , z ) = \sum _ { i = m } ^ { N } P _ { i } ( v ) z ^ { i }$ ; confidence 0.697

290. 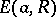 ; $E ( a , R )$ ; confidence 0.696

291.  ; $\mathbf{C} \times ( \mathbf{C} \backslash ( - \infty , 0 ) )$ ; confidence 0.696

292. 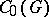 ; $C _ { 0 } ( G )$ ; confidence 0.696

293.  ; $F _ { n+1 } \rightarrow F _ { n }$ ; confidence 0.696

294. 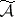 ; $\tilde { A }$ ; confidence 0.696

295. 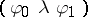 ; $( \varphi _ { 0 } \lambda \varphi _ { 1 } )$ ; confidence 0.696

296.  ; $\operatorname { per } ( A ) \geq \operatorname { per } ( B ) \operatorname { per } ( D ) \geq \prod _ { i = 1 } ^ { n } a _ { i i }.$ ; confidence 0.696

297.  ; $A \mathbf{x} \leq \mathbf{b} + \varepsilon$ ; confidence 0.696

298. 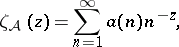 ; $\zeta _ { A } ( z ) = \sum _ { n = 1 } ^ { \infty } a ( n ) n ^ { - z },$ ; confidence 0.696

299. 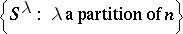 ; $\left\{ S ^ { \lambda } : \lambda \text { a partition of } n \right\}$ ; confidence 0.696

300. 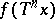 ; $f ( T ^ { n } x )$ ; confidence 0.696