User:Maximilian Janisch/latexlist/latex/19
List
1. 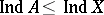 ; $A < \operatorname { ln } d X$ ; confidence 0.106
; $A < \operatorname { ln } d X$ ; confidence 0.106
2. 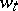 ; $M _ { t }$ ; confidence 0.106
; $M _ { t }$ ; confidence 0.106
3. 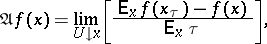 ; $\mathfrak { A } f ( x ) = \operatorname { lim } _ { U ! x } [ \frac { E _ { x } f ( x _ { \tau } ) - f ( x ) } { E _ { x } \tau } ]$ ; confidence 0.104
; $\mathfrak { A } f ( x ) = \operatorname { lim } _ { U ! x } [ \frac { E _ { x } f ( x _ { \tau } ) - f ( x ) } { E _ { x } \tau } ]$ ; confidence 0.104
4. 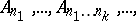 ; $x _ { 1 } , \ldots , A _ { x _ { 1 } } \ldots x _ { k } , \ldots ,$ ; confidence 0.104
; $x _ { 1 } , \ldots , A _ { x _ { 1 } } \ldots x _ { k } , \ldots ,$ ; confidence 0.104
5. 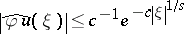 ; $| \tilde { \varphi } \mathfrak { u } ( \xi ) | \leq c ^ { - 1 } e ^ { - c | \xi | ^ { 1 / s } }$ ; confidence 0.103
; $| \tilde { \varphi } \mathfrak { u } ( \xi ) | \leq c ^ { - 1 } e ^ { - c | \xi | ^ { 1 / s } }$ ; confidence 0.103
6.  ; $F ( t | S ) = F ( a ( t ) | S _ { y } ) , \quad t \geq 0$ ; confidence 0.102
; $F ( t | S ) = F ( a ( t ) | S _ { y } ) , \quad t \geq 0$ ; confidence 0.102
7. 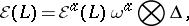 ; $E ( L ) = E ^ { d } ( L ) \omega ^ { \alpha } \bigotimes \Delta$ ; confidence 0.101
; $E ( L ) = E ^ { d } ( L ) \omega ^ { \alpha } \bigotimes \Delta$ ; confidence 0.101
8. 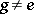 ; $g \neq \theta$ ; confidence 0.098
; $g \neq \theta$ ; confidence 0.098
9. 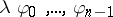 ; $\lambda \varphi 0 , \ldots , \varphi _ { x } - 1$ ; confidence 0.095
; $\lambda \varphi 0 , \ldots , \varphi _ { x } - 1$ ; confidence 0.095
10. 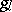 ; $Q$ ; confidence 0.095
; $Q$ ; confidence 0.095
11. 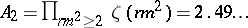 ; $A _ { 2 } = \prod _ { m _ { 2 } } ^ { 2 } \geq 2 \zeta ( m ^ { 2 } ) = 2.49$ ; confidence 0.094
; $A _ { 2 } = \prod _ { m _ { 2 } } ^ { 2 } \geq 2 \zeta ( m ^ { 2 } ) = 2.49$ ; confidence 0.094
12. 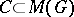 ; $\operatorname { Ccm } ( G )$ ; confidence 0.094
; $\operatorname { Ccm } ( G )$ ; confidence 0.094
13. 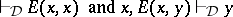 ; $\operatorname { Id } E ( x , x ) \text { and } x , E ( x , y ) | _ { D } y$ ; confidence 0.093
; $\operatorname { Id } E ( x , x ) \text { and } x , E ( x , y ) | _ { D } y$ ; confidence 0.093
14. 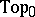 ; $\operatorname { sin } 0$ ; confidence 0.092
; $\operatorname { sin } 0$ ; confidence 0.092
15. 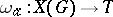 ; $\omega _ { \mathscr { A } } : X ( G ) \rightarrow T$ ; confidence 0.090
; $\omega _ { \mathscr { A } } : X ( G ) \rightarrow T$ ; confidence 0.090
16. 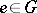 ; $\varepsilon \in C$ ; confidence 0.090
; $\varepsilon \in C$ ; confidence 0.090
17. 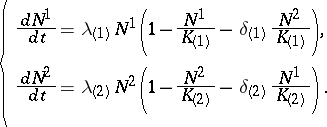 ; $\left. \begin{array}{l}{ \frac { d N ^ { 1 } } { d t } = \lambda _ { ( 1 ) } N ^ { 1 } ( 1 - \frac { N ^ { 1 } } { K _ { ( 1 ) } } - \delta _ { ( 1 ) } \frac { N ^ { 2 } } { K _ { ( 1 ) } } ) }\\{ \frac { d N ^ { 2 } } { d t } = \lambda _ { ( 2 ) } N ^ { 2 } ( 1 - \frac { N ^ { 2 } } { K _ { ( 2 ) } } - \delta _ { ( 2 ) } \frac { N ^ { 1 } } { K _ { ( 2 ) } } ) }\end{array} \right.$ ; confidence 0.089
; $\left. \begin{array}{l}{ \frac { d N ^ { 1 } } { d t } = \lambda _ { ( 1 ) } N ^ { 1 } ( 1 - \frac { N ^ { 1 } } { K _ { ( 1 ) } } - \delta _ { ( 1 ) } \frac { N ^ { 2 } } { K _ { ( 1 ) } } ) }\\{ \frac { d N ^ { 2 } } { d t } = \lambda _ { ( 2 ) } N ^ { 2 } ( 1 - \frac { N ^ { 2 } } { K _ { ( 2 ) } } - \delta _ { ( 2 ) } \frac { N ^ { 1 } } { K _ { ( 2 ) } } ) }\end{array} \right.$ ; confidence 0.089
18. 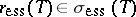 ; $r _ { e . s s } ( T ) \in \sigma _ { ess } ( T )$ ; confidence 0.088
; $r _ { e . s s } ( T ) \in \sigma _ { ess } ( T )$ ; confidence 0.088
19. 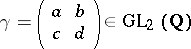 ; $\gamma = \left( \begin{array} { l l } { \alpha } & { b } \\ { c } & { d } \end{array} \right) \in GL _ { 2 } ( Q )$ ; confidence 0.088
; $\gamma = \left( \begin{array} { l l } { \alpha } & { b } \\ { c } & { d } \end{array} \right) \in GL _ { 2 } ( Q )$ ; confidence 0.088
20. 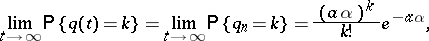 ; $\operatorname { lim } _ { t \rightarrow \infty } P \{ q ( t ) = k \} = \operatorname { lim } _ { t \rightarrow \infty } P \{ q _ { n } = k \} = \frac { ( \alpha \alpha ) ^ { k } } { k ! } e ^ { - \alpha ^ { \prime } \alpha }$ ; confidence 0.087
; $\operatorname { lim } _ { t \rightarrow \infty } P \{ q ( t ) = k \} = \operatorname { lim } _ { t \rightarrow \infty } P \{ q _ { n } = k \} = \frac { ( \alpha \alpha ) ^ { k } } { k ! } e ^ { - \alpha ^ { \prime } \alpha }$ ; confidence 0.087
21. 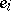 ; $E _ { i }$ ; confidence 0.085
; $E _ { i }$ ; confidence 0.085
22.  ; $\eta : \pi _ { N } \otimes \pi _ { N } \rightarrow \pi _ { N } + 1$ ; confidence 0.085
; $\eta : \pi _ { N } \otimes \pi _ { N } \rightarrow \pi _ { N } + 1$ ; confidence 0.085
23. 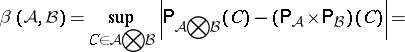 ; $\beta ( A , B ) = \operatorname { sup } _ { C \in A \otimes B } | P _ { A \otimes B } ( C ) - ( P _ { A } \times P _ { B } ) ( C ) | =$ ; confidence 0.084
; $\beta ( A , B ) = \operatorname { sup } _ { C \in A \otimes B } | P _ { A \otimes B } ( C ) - ( P _ { A } \times P _ { B } ) ( C ) | =$ ; confidence 0.084
24. 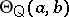 ; $O ( a , b )$ ; confidence 0.083
; $O ( a , b )$ ; confidence 0.083
25. 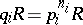 ; $q _ { k } R = p _ { j } ^ { n _ { i } } R _ { R }$ ; confidence 0.083
; $q _ { k } R = p _ { j } ^ { n _ { i } } R _ { R }$ ; confidence 0.083
26. 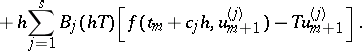 ; $+ h \sum _ { j = 1 } ^ { s } B _ { j } ( h T ) [ f ( t _ { m } + c _ { j } h , u _ { m + 1 } ^ { ( j ) } ) - T u _ { m j } ^ { ( j ) } + 1 ]$ ; confidence 0.083
; $+ h \sum _ { j = 1 } ^ { s } B _ { j } ( h T ) [ f ( t _ { m } + c _ { j } h , u _ { m + 1 } ^ { ( j ) } ) - T u _ { m j } ^ { ( j ) } + 1 ]$ ; confidence 0.083
27. 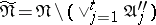 ; $\tilde { \mathfrak { N } } = \mathfrak { N } \backslash ( V _ { j = 1 } ^ { t } \mathfrak { A } ^ { \prime \prime } )$ ; confidence 0.082
; $\tilde { \mathfrak { N } } = \mathfrak { N } \backslash ( V _ { j = 1 } ^ { t } \mathfrak { A } ^ { \prime \prime } )$ ; confidence 0.082
28. 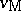 ; $V _ { V }$ ; confidence 0.082
; $V _ { V }$ ; confidence 0.082
29. 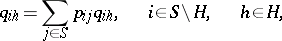 ; $q _ { i h } = \sum _ { j \in S } p _ { i } q _ { h } , \quad i \in S \backslash H , \quad h \in H$ ; confidence 0.082
; $q _ { i h } = \sum _ { j \in S } p _ { i } q _ { h } , \quad i \in S \backslash H , \quad h \in H$ ; confidence 0.082
30. 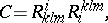 ; $C = R _ { k m m } ^ { i } R _ { k } ^ { k k m }$ ; confidence 0.081
; $C = R _ { k m m } ^ { i } R _ { k } ^ { k k m }$ ; confidence 0.081
31. 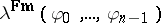 ; $\lambda ^ { F m } ( \varphi 0 , \dots , \varphi _ { m } - 1 )$ ; confidence 0.080
; $\lambda ^ { F m } ( \varphi 0 , \dots , \varphi _ { m } - 1 )$ ; confidence 0.080
32. 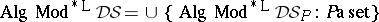 ; $^ { * } L D S = \cup \{ \text { Alg } Mod ^ { * } L D S _ { P } : \text { Paset } \}$ ; confidence 0.080
; $^ { * } L D S = \cup \{ \text { Alg } Mod ^ { * } L D S _ { P } : \text { Paset } \}$ ; confidence 0.080
33. 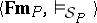 ; $\langle F m _ { P } , \operatorname { mod } e l s s _ { P } \rangle$ ; confidence 0.080
; $\langle F m _ { P } , \operatorname { mod } e l s s _ { P } \rangle$ ; confidence 0.080
34. 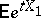 ; $E _ { e } ^ { t X } 1$ ; confidence 0.078
; $E _ { e } ^ { t X } 1$ ; confidence 0.078
35. 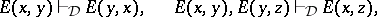 ; $E ( x , y ) \nmid _ { D } E ( y , x ) , \quad E ( x , y ) , E ( y , z ) | _ { D } E ( x , z )$ ; confidence 0.078
; $E ( x , y ) \nmid _ { D } E ( y , x ) , \quad E ( x , y ) , E ( y , z ) | _ { D } E ( x , z )$ ; confidence 0.078
36.  ; $1$ ; confidence 0.077
; $1$ ; confidence 0.077
37.  ; $\mathfrak { C } 1 , \ldots , \mathfrak { C } _ { x }$ ; confidence 0.076
; $\mathfrak { C } 1 , \ldots , \mathfrak { C } _ { x }$ ; confidence 0.076
38. 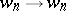 ; $W _ { N } \rightarrow W _ { n }$ ; confidence 0.076
; $W _ { N } \rightarrow W _ { n }$ ; confidence 0.076
39. 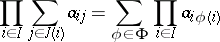 ; $\prod _ { i \in I } \sum _ { j \in J ( i ) } \alpha _ { i j } = \sum _ { \phi \in \Phi } \prod _ { i \in I } \alpha _ { i \phi ( i ) }$ ; confidence 0.076
; $\prod _ { i \in I } \sum _ { j \in J ( i ) } \alpha _ { i j } = \sum _ { \phi \in \Phi } \prod _ { i \in I } \alpha _ { i \phi ( i ) }$ ; confidence 0.076
40. 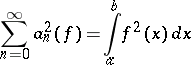 ; $\sum _ { n = 0 } ^ { \infty } a _ { \tilde { m } } ^ { 2 } ( f ) = \int _ { \mathscr { x } } ^ { b } f ^ { 2 } ( x ) d x$ ; confidence 0.076
; $\sum _ { n = 0 } ^ { \infty } a _ { \tilde { m } } ^ { 2 } ( f ) = \int _ { \mathscr { x } } ^ { b } f ^ { 2 } ( x ) d x$ ; confidence 0.076
41. 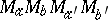 ; $M _ { \mathscr { C } } M _ { b } M _ { \alpha ^ { \prime } } M _ { \phi }$ ; confidence 0.076
; $M _ { \mathscr { C } } M _ { b } M _ { \alpha ^ { \prime } } M _ { \phi }$ ; confidence 0.076
42. 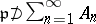 ; $\mathfrak { p } \not p \not \sum _ { n = 1 } ^ { \infty } A _ { n }$ ; confidence 0.075
; $\mathfrak { p } \not p \not \sum _ { n = 1 } ^ { \infty } A _ { n }$ ; confidence 0.075
43. 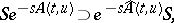 ; $S _ { e } ^ { - s A ( t , u ) } \supset e ^ { - s A ( t , u ) } S$ ; confidence 0.075
; $S _ { e } ^ { - s A ( t , u ) } \supset e ^ { - s A ( t , u ) } S$ ; confidence 0.075
44.  ; $I _ { A / P } ^ { B }$ ; confidence 0.075
; $I _ { A / P } ^ { B }$ ; confidence 0.075
45. 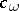 ; $C _ { \omega }$ ; confidence 0.073
; $C _ { \omega }$ ; confidence 0.073
46. 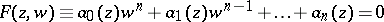 ; $F ( z , w ) \equiv \alpha _ { 0 } ( z ) w ^ { \prime \prime } + \alpha _ { 1 } ( z ) w ^ { \prime \prime } - 1 + \ldots + \alpha _ { x } ( z ) = 0$ ; confidence 0.073
; $F ( z , w ) \equiv \alpha _ { 0 } ( z ) w ^ { \prime \prime } + \alpha _ { 1 } ( z ) w ^ { \prime \prime } - 1 + \ldots + \alpha _ { x } ( z ) = 0$ ; confidence 0.073
47. 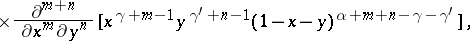 ; $\times \frac { \partial ^ { m + n } } { \partial x ^ { m } \partial y ^ { n } } [ x ^ { \gamma + m - 1 } y ^ { \prime } + n - 1 _ { ( 1 - x - y ) } \alpha + w + n - \gamma - \gamma ^ { \prime } ]$ ; confidence 0.072
; $\times \frac { \partial ^ { m + n } } { \partial x ^ { m } \partial y ^ { n } } [ x ^ { \gamma + m - 1 } y ^ { \prime } + n - 1 _ { ( 1 - x - y ) } \alpha + w + n - \gamma - \gamma ^ { \prime } ]$ ; confidence 0.072
48.  ; $J = \left| \begin{array} { c c c c } { J _ { n _ { 1 } } ( \lambda _ { 1 } ) } & { \square } & { \square } & { \square } \\ { \square } & { \ldots } & { \square } & { 0 } \\ { 0 } & { \square } & { \ldots } & { \square } \\ { \square } & { \square } & { \square } & { J _ { n _ { S } } ( \lambda _ { s } ) } \end{array} \right|$ ; confidence 0.072
; $J = \left| \begin{array} { c c c c } { J _ { n _ { 1 } } ( \lambda _ { 1 } ) } & { \square } & { \square } & { \square } \\ { \square } & { \ldots } & { \square } & { 0 } \\ { 0 } & { \square } & { \ldots } & { \square } \\ { \square } & { \square } & { \square } & { J _ { n _ { S } } ( \lambda _ { s } ) } \end{array} \right|$ ; confidence 0.072
49. 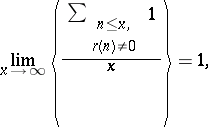 ; $\operatorname { lim } _ { x \rightarrow \infty } \left( \begin{array} { c } { \sum _ { n \leq x , n \atop x } 1 } \\ { \frac { n ( n ) \neq 0 } { x } } \end{array} \right) = 1$ ; confidence 0.072
; $\operatorname { lim } _ { x \rightarrow \infty } \left( \begin{array} { c } { \sum _ { n \leq x , n \atop x } 1 } \\ { \frac { n ( n ) \neq 0 } { x } } \end{array} \right) = 1$ ; confidence 0.072
50. 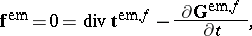 ; $f ^ { em } = 0 = \operatorname { div } t ^ { em } f - \frac { \partial G ^ { em f } } { \partial t }$ ; confidence 0.071
; $f ^ { em } = 0 = \operatorname { div } t ^ { em } f - \frac { \partial G ^ { em f } } { \partial t }$ ; confidence 0.071
51. 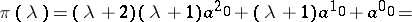 ; $\pi ( \lambda ) = ( \lambda + 2 ) ( \lambda + 1 ) \alpha ^ { 2 } 0 + ( \lambda + 1 ) \alpha ^ { 1 } 0 + a ^ { 0 } =$ ; confidence 0.071
; $\pi ( \lambda ) = ( \lambda + 2 ) ( \lambda + 1 ) \alpha ^ { 2 } 0 + ( \lambda + 1 ) \alpha ^ { 1 } 0 + a ^ { 0 } =$ ; confidence 0.071
52. 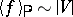 ; $\{ f \rangle _ { P } \sim | V |$ ; confidence 0.071
; $\{ f \rangle _ { P } \sim | V |$ ; confidence 0.071
53. 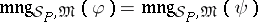 ; $g _ { S _ { P } , \mathfrak { M } } ( \varphi ) = \operatorname { mng } _ { S } _ { P } , \mathfrak { M } ( \psi )$ ; confidence 0.071
; $g _ { S _ { P } , \mathfrak { M } } ( \varphi ) = \operatorname { mng } _ { S } _ { P } , \mathfrak { M } ( \psi )$ ; confidence 0.071
54.  ; $t _ { G } \theta _ { 0 } , \ldots , \theta _ { n - 1 } \gg \xi$ ; confidence 0.070
; $t _ { G } \theta _ { 0 } , \ldots , \theta _ { n - 1 } \gg \xi$ ; confidence 0.070
55. 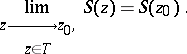 ; $z \frac { \operatorname { lim } } { z \rightarrow z _ { 0 } } \quad S ( z ) = S ( z 0 )$ ; confidence 0.069
; $z \frac { \operatorname { lim } } { z \rightarrow z _ { 0 } } \quad S ( z ) = S ( z 0 )$ ; confidence 0.069
56. 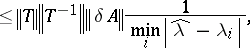 ; $\leq \| T \| ^ { T ^ { - 1 } } \| \| \delta A \| \frac { 1 } { \operatorname { min } } | \hat { \lambda } - \lambda _ { i } |$ ; confidence 0.069
; $\leq \| T \| ^ { T ^ { - 1 } } \| \| \delta A \| \frac { 1 } { \operatorname { min } } | \hat { \lambda } - \lambda _ { i } |$ ; confidence 0.069
57. 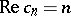 ; $\operatorname { Re } _ { c _ { N } } = n$ ; confidence 0.069
; $\operatorname { Re } _ { c _ { N } } = n$ ; confidence 0.069
58. 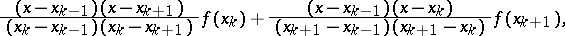 ; $\frac { ( x - x _ { k } - 1 ) ( x - x _ { k + 1 } ) } { ( x _ { k } - x _ { k - 1 } ) ( x _ { k } - x _ { k + 1 } ) } f ( x _ { k } ) + \frac { ( x - x _ { k - 1 } ) ( x - x _ { k } ) } { ( x _ { k } + 1 - x _ { k - 1 } ) ( x _ { k + 1 } - x _ { k } ) } f ( x _ { k + 1 } )$ ; confidence 0.069
; $\frac { ( x - x _ { k } - 1 ) ( x - x _ { k + 1 } ) } { ( x _ { k } - x _ { k - 1 } ) ( x _ { k } - x _ { k + 1 } ) } f ( x _ { k } ) + \frac { ( x - x _ { k - 1 } ) ( x - x _ { k } ) } { ( x _ { k } + 1 - x _ { k - 1 } ) ( x _ { k + 1 } - x _ { k } ) } f ( x _ { k + 1 } )$ ; confidence 0.069
59. 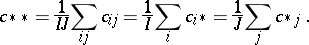 ; $c * x = \frac { 1 } { I J } \sum _ { i j } c _ { j } = \frac { 1 } { I } \sum _ { i } c _ { i } x = \frac { 1 } { J } \sum _ { j } c * j$ ; confidence 0.068
; $c * x = \frac { 1 } { I J } \sum _ { i j } c _ { j } = \frac { 1 } { I } \sum _ { i } c _ { i } x = \frac { 1 } { J } \sum _ { j } c * j$ ; confidence 0.068
60. 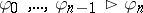 ; $\varphi _ { 0 } , \ldots , \varphi _ { n - 1 } \gg \varphi _ { n }$ ; confidence 0.068
; $\varphi _ { 0 } , \ldots , \varphi _ { n - 1 } \gg \varphi _ { n }$ ; confidence 0.068
61. 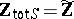 ; $Z _ { \text { tot } S } = Z$ ; confidence 0.066
; $Z _ { \text { tot } S } = Z$ ; confidence 0.066
62. 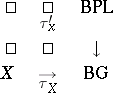 ; $\left. \begin{array} { c c c } { \square } & { \square } & { B P L } \\ { \square } & { \square } & { \downarrow } \\ { X } & { \vec { \tau } _ { X } } & { B G } \end{array} \right.$ ; confidence 0.066
; $\left. \begin{array} { c c c } { \square } & { \square } & { B P L } \\ { \square } & { \square } & { \downarrow } \\ { X } & { \vec { \tau } _ { X } } & { B G } \end{array} \right.$ ; confidence 0.066
63. 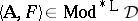 ; $\langle A , F \rangle \in M od ^ { * } L D$ ; confidence 0.065
; $\langle A , F \rangle \in M od ^ { * } L D$ ; confidence 0.065
64. 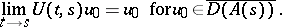 ; $\operatorname { lim } _ { t \rightarrow S } U ( t , s ) u _ { 0 } = u _ { 0 } \text { for } u _ { 0 } \in \overline { D ( A ( s ) ) }$ ; confidence 0.064
; $\operatorname { lim } _ { t \rightarrow S } U ( t , s ) u _ { 0 } = u _ { 0 } \text { for } u _ { 0 } \in \overline { D ( A ( s ) ) }$ ; confidence 0.064
65. 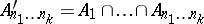 ; $A _ { x _ { 1 } } ^ { \prime } \ldots x _ { k } = A _ { 1 } \cap \ldots \cap A _ { x _ { 1 } } \ldots x _ { k }$ ; confidence 0.061
; $A _ { x _ { 1 } } ^ { \prime } \ldots x _ { k } = A _ { 1 } \cap \ldots \cap A _ { x _ { 1 } } \ldots x _ { k }$ ; confidence 0.061
66. 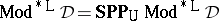 ; $^ { * } L D = S PP _ { U } Mod ^ { * } L _ { D }$ ; confidence 0.061
; $^ { * } L D = S PP _ { U } Mod ^ { * } L _ { D }$ ; confidence 0.061
67.  ; $C ^ { 4 } P ^ { 3 }$ ; confidence 0.060
; $C ^ { 4 } P ^ { 3 }$ ; confidence 0.060
68. 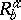 ; $R _ { y } ^ { t }$ ; confidence 0.060
; $R _ { y } ^ { t }$ ; confidence 0.060
69. 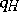 ; $Q _ { 1 }$ ; confidence 0.060
; $Q _ { 1 }$ ; confidence 0.060
70. 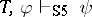 ; $T , \varphi \operatorname { log } 5 \psi$ ; confidence 0.060
; $T , \varphi \operatorname { log } 5 \psi$ ; confidence 0.060
71. 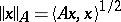 ; $\| x \| _ { A } = \langle A x , x \rangle ^ { 1 / 2 }$ ; confidence 0.059
; $\| x \| _ { A } = \langle A x , x \rangle ^ { 1 / 2 }$ ; confidence 0.059
72.  ; $\alpha ^ { \psi } = Op ( J ^ { 1 / 2 } \alpha )$ ; confidence 0.058
; $\alpha ^ { \psi } = Op ( J ^ { 1 / 2 } \alpha )$ ; confidence 0.058
73.  ; $\delta _ { \lambda } ( t ) \psi ^ { ( x , y ) _ { \nu } } ( t )$ ; confidence 0.057
; $\delta _ { \lambda } ( t ) \psi ^ { ( x , y ) _ { \nu } } ( t )$ ; confidence 0.057
74. 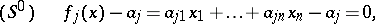 ; $\quad f j ( x ) - \alpha j = \alpha _ { j 1 } x _ { 1 } + \ldots + \alpha _ { j n } x _ { n } - \alpha _ { j } = 0$ ; confidence 0.057
; $\quad f j ( x ) - \alpha j = \alpha _ { j 1 } x _ { 1 } + \ldots + \alpha _ { j n } x _ { n } - \alpha _ { j } = 0$ ; confidence 0.057
75. 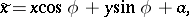 ; $x = x \operatorname { cos } \phi + y \operatorname { sin } \phi + \alpha$ ; confidence 0.056
; $x = x \operatorname { cos } \phi + y \operatorname { sin } \phi + \alpha$ ; confidence 0.056
76. 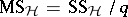 ; $= \operatorname { sin } \gamma q$ ; confidence 0.055
; $= \operatorname { sin } \gamma q$ ; confidence 0.055
77. 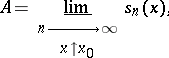 ; $A = \underbrace { \operatorname { lim } _ { n } \frac { \operatorname { lim } } { x \nmid x _ { 0 } } } s _ { n } ( x )$ ; confidence 0.055
; $A = \underbrace { \operatorname { lim } _ { n } \frac { \operatorname { lim } } { x \nmid x _ { 0 } } } s _ { n } ( x )$ ; confidence 0.055
78. 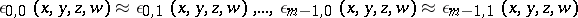 ; $\epsilon 0,0 ( x , y , z , w ) \approx \epsilon 0,1 ( x , y , z , w ) , \ldots , \epsilon _ { m - 1,0 } ( x , y , z , w ) \approx \epsilon _ { m - 1 } , 1 ( x , y , z , w )$ ; confidence 0.055
; $\epsilon 0,0 ( x , y , z , w ) \approx \epsilon 0,1 ( x , y , z , w ) , \ldots , \epsilon _ { m - 1,0 } ( x , y , z , w ) \approx \epsilon _ { m - 1 } , 1 ( x , y , z , w )$ ; confidence 0.055
79. 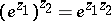 ; $( e ^ { z } 1 ) ^ { z } = e ^ { z } 1 ^ { z _ { 2 } }$ ; confidence 0.053
; $( e ^ { z } 1 ) ^ { z } = e ^ { z } 1 ^ { z _ { 2 } }$ ; confidence 0.053
80. 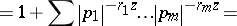 ; $= 1 + \sum | p _ { 1 } | ^ { - r _ { 1 } z } \ldots | p _ { x _ { 2 } } | ^ { - r _ { m } z } =$ ; confidence 0.052
; $= 1 + \sum | p _ { 1 } | ^ { - r _ { 1 } z } \ldots | p _ { x _ { 2 } } | ^ { - r _ { m } z } =$ ; confidence 0.052
81. 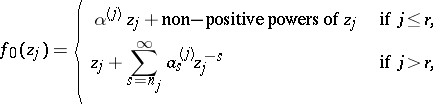 ; $f _ { 0 } ( z _ { j } ) = \left\{ \begin{array} { l l } { \alpha ^ { ( j ) } z _ { j } + \text { non-positive powers of } z _ { j } } & { \text { if } j \leq r } \\ { z _ { j } + \sum _ { s = x _ { j } } ^ { \infty } a _ { s } ^ { ( j ) } z _ { j } ^ { - s } } & { \text { if } j > r } \end{array} \right.$ ; confidence 0.051
; $f _ { 0 } ( z _ { j } ) = \left\{ \begin{array} { l l } { \alpha ^ { ( j ) } z _ { j } + \text { non-positive powers of } z _ { j } } & { \text { if } j \leq r } \\ { z _ { j } + \sum _ { s = x _ { j } } ^ { \infty } a _ { s } ^ { ( j ) } z _ { j } ^ { - s } } & { \text { if } j > r } \end{array} \right.$ ; confidence 0.051
82. 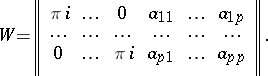 ; $W = \left\| \begin{array} { c c c c c c } { \pi i } & { \ldots } & { 0 } & { a _ { 11 } } & { \ldots } & { a _ { 1 p } } \\ { \cdots } & { \cdots } & { \cdots } & { \cdots } & { \cdots } & { \cdots } \\ { 0 } & { \ldots } & { \pi i } & { a _ { p 1 } } & { \ldots } & { a _ { p p } } \end{array} \right\|$ ; confidence 0.051
; $W = \left\| \begin{array} { c c c c c c } { \pi i } & { \ldots } & { 0 } & { a _ { 11 } } & { \ldots } & { a _ { 1 p } } \\ { \cdots } & { \cdots } & { \cdots } & { \cdots } & { \cdots } & { \cdots } \\ { 0 } & { \ldots } & { \pi i } & { a _ { p 1 } } & { \ldots } & { a _ { p p } } \end{array} \right\|$ ; confidence 0.051
83. 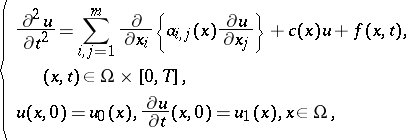 ; $\left. \begin{array}{l}{ \frac { \partial ^ { 2 } u } { \partial t ^ { 2 } } = \sum _ { i , j = 1 } ^ { m } \frac { \partial } { \partial x _ { i } } \{ \alpha _ { j } , ( x ) \frac { \partial u } { \partial x _ { j } } \} + c ( x ) u + f ( x , t ) }\\{ ( x , t ) \in \Omega \times [ 0 , T ] }\\{ u ( x , 0 ) = u _ { 0 } ( x ) , \frac { \partial u } { \partial t } ( x , 0 ) = u _ { 1 } ( x ) , x \in \Omega }\end{array} \right.$ ; confidence 0.050
; $\left. \begin{array}{l}{ \frac { \partial ^ { 2 } u } { \partial t ^ { 2 } } = \sum _ { i , j = 1 } ^ { m } \frac { \partial } { \partial x _ { i } } \{ \alpha _ { j } , ( x ) \frac { \partial u } { \partial x _ { j } } \} + c ( x ) u + f ( x , t ) }\\{ ( x , t ) \in \Omega \times [ 0 , T ] }\\{ u ( x , 0 ) = u _ { 0 } ( x ) , \frac { \partial u } { \partial t } ( x , 0 ) = u _ { 1 } ( x ) , x \in \Omega }\end{array} \right.$ ; confidence 0.050
Maximilian Janisch/latexlist/latex/19. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Maximilian_Janisch/latexlist/latex/19&oldid=43926