Period of a function

A number such that for any (or ) the numbers and also belong to and such that the following equality holds:

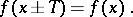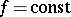The numbers , where is a natural number, are also periods of . For a function on an axis or on a plane, any number 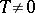is a period; for the Dirichlet function

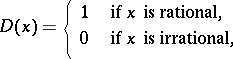any rational number is a period. If a function 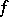has period 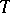, then the function 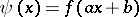, where and 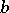are constants and 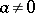, has period 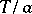. If a real-valued function 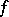of a real argument is continuous and periodic on 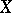(and is not identically equal to a constant), then it has a least period 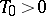and any other real period is a multiple of 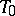. There exist non-constant functions of a complex argument having two non-multiple periods with imaginary quotient, such as for example an elliptic function.

Similarly one defines the period of a function defined on an Abelian group.

Comments

Cf. also Periodic function.