Angle
A geometrical figure consisting of two distinct rays issuing from the same point. The rays are called the sides of the angle, and their common original is called the vertex of the angle. Let $ [BA),[BC) $ denote the sides of an angle, $ B $ its vertex, and $ \alpha $ the plane defined by its sides. The figure $ \Gamma = [BA) \cup [BC) $ divides the plane $ \alpha $ into two adjoint regions $ \alpha'_{i} $, $ i \in \{ 1,2 \} $: $ \alpha'_{1} \cup \alpha'_{2} = \alpha \setminus \Gamma $. The region $ \alpha_{i} = \alpha'_{i} \cup \Gamma $, $ i \in \{ 1,2 \} $, is also called an angle or a plane angle, $ \alpha'_{i} $ is called the interior domain of the plane angle $ \alpha_{i} $. The regions (angles) $ \alpha_{1},\alpha_{2} $ are called supplementary.
Two angles are called equal (or congruent) if they can be superposed so that corresponding sides and vertices coincides. For every ray in the plane and a given side of it, one can construct a unique angle equal to a given one. The comparison of two angles can be realized in two ways. If the angle is considered as a pair of rays with a common origin, then to answer the question which of the two angles is the greater, it is necessary to superpose in the given plane the vertices and one of each pair of sides (see Figure (a)). If the second side of an angle comes to lie inside the second angle, one says that the first angle is smaller than the second.
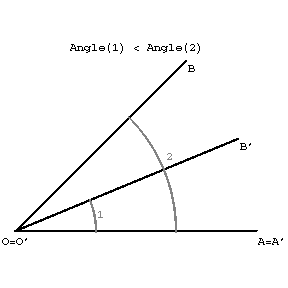
Figure (a)
A second method of comparing angles consists in assigning to each angle a certain number. Equal angles will have the same number of degrees or radians (see below), greater angles a greater and smaller angles a smaller number.
Two angles are called supplementary if they have their vertex and one side is common, while the other two sides form a straight line (see Figure (b)).
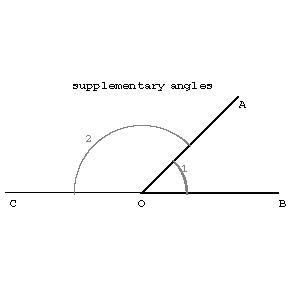
Figure (b)
Generally, angles having a common vertex and one common side are called adjoining. Two angles are called vertical if the sides of one are the prolongations through the vertex of the sides of the other. Vertical angles are equal to each other. Angles the sides of which form a straight line are called straight. Half a straight angle is called a right angle. A right angle may equivalently be defined as follows: An angle equal to its supplement is called right. The interior domain of a plane angle that is not greater then a straight angle is called a convex domain in the plane.
As the unit of measurement of an angle, one uses the $ 90 $th part of a right angle, called a degree. The cyclic or radian measure of an angle is also used. The numerical value of the radian measure of an angle is the length of the arc cut out by the sides of the angle on the unit circle. One radian is assigned to the angle the arc of which has length equal to the radius. A straight angle is equal to $ \pi $ radians.
By intersecting two straight lines lying in a plane with a third, there are formed angles (see Figure (c)): 1 and 5, 2 and 6, 4 and 8, 3 and 7; these are called corresponding angles; 2 and 5, 3 and 8 are called interior angles on the same side; 1 and 6, 4 and 7 are called exterior angles on the same side; 3 and 5, 2 and 8 are called interior opposite angles; and 1 and 7, 4 and 6 are called exterior opposite angles.
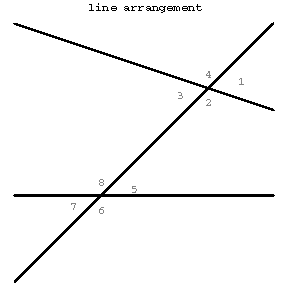
Figure (c)
In practical problems, it is convenient to consider angles as the measure of rotation of a fixed ray round its origin to a given position. Depending on the direction of the rotation, the angle may in this case be considered as positive or negative. Thus, an angle in this sense can have as value any real number. The angle as a measure of the rotation of a ray is considered in the theory of trigonometric functions: For any value of the argument (an angle), one can define a value for the trigonometric functions. The concept of an angle in geometrical systems founded on the axiomatics of positions of point vectors is radically different from the definition of angles as figures — in such axiomatics, by an angle, one understands a well-defined metric quantity connected with two vectors by means of their scalar product. Thus, each pair $ (\mathbf{a},\mathbf{b}) $ of vectors defines a certain angle $ \phi $ — the number given by the vector formula $$ \cos(\phi) = \frac{\langle \mathbf{a},\mathbf{b} \rangle}{\| \mathbf{a} \| \| \mathbf{b} \|}, $$ where $ \langle \mathbf{a},\mathbf{b} \rangle $ is the scalar product of the vectors.
The concept of an angle as a plane figure and as a certain numerical quantity is applied in different geometrical problems in which the angle plays a special role. Thus, by the angle between two intersecting curves having a well-defined tangent in their point of intersection one understands the angle formed by these tangents.
By the angle between a straight line and a plane, one understands the angle formed by the straight line and its orthogonal projection on the plane; its value lies between $ 0^{\circ} $ and $ 90^{\circ} $. By the angle between two crossing lines, one understands the angle between the directions of these lines, i.e., between two lines parallel to the given crossing lines and passing through a given point.
A solid angle is a part of space bounding a certain conical surface; a particular case of a solid angle is a polyhedral angle.
In higher-dimensional geometry, one defines the angle between multi-dimensional planes, between straight lines and planes, etc. Angles between straight lines, between planes and straight lines, and between higher-dimensional planes are also defined in non-Euclidean spaces.
References
| [a1] | M.J. Greenberg, “Euclidean and non-Euclidean geometries”, Freeman (1974). |
Angle. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Angle&oldid=39910