Cauchy test

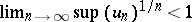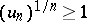The Cauchy criterion for the convergence of a series: Given a series $\sum_{n=1}^{\infty}u_n$ with non-negative real terms, if there exists a number $q$, $0\leq q<1$, such that, for all sufficiently large $n$, one has the inequality $(u_n)^{1/n}\leq q$, which is equivalent to the condition , then the series is convergent. Conversely, if for all sufficiently large one has the inequality , or even the weaker condition: There exists a subsequence 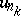, 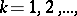with terms satisfying the inequality 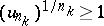, then the series is divergent.

In particular, if 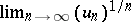exists and is 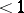, then the series 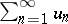is convergent; if it is 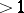, then the series 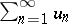is divergent. This was proved by A.L. Cauchy . In the case of a series 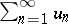with terms 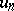of arbitrary sign, the condition 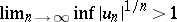implies that the series is divergent; if 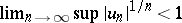, the series is absolutely convergent.

The integral Cauchy test, or the Cauchy–MacLaurin integral criterion: Given a series 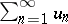with non-negative real terms, if there exists a non-increasing non-negative function 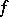, defined for 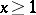, such that 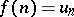, 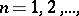then the series is convergent if and only if the integral 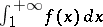is convergent. This test was first presented in a geometrical form by C. MacLaurin [2], and later rediscovered by A.L. Cauchy [3].

References

[1]	A.L. Cauchy, "Analyse algébrique" , Gauthier-Villars (1821) pp. 132–135 (German translation: Springer, 1885)
[2]	C. MacLaurin, "Treatise of fluxions" , 1 , Edinburgh (1742) pp. 289–290
[3]	A.L. Cauchy, "Sur la convergence des séries" , Oeuvres complètes Ser. 2 , 7 , Gauthier-Villars (1889) pp. 267–279
[4]	S.M. Nikol'skii, "A course of mathematical analysis" , 1 , MIR (1977) (Translated from Russian)

Comments

See also Cauchy criteria. The following is also known as Cauchy's condensation test or Cauchy's convergence theorem (criterion): If the terms 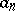of a series 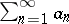form a monotone decreasing sequence, then 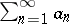and

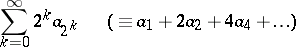are equiconvergent series, i.e. both converge or both diverge (cf. [a1], [a2]).

References

[a1]	K. Knopp, "Theorie und Anwendung der unendlichen Reihen" , Springer (1964) (English translation: Blackie, 1951 & Dover, reprint, 1990)
[a2]	G.H. Hardy, "A course of pure mathematics" , Cambridge Univ. Press (1975)