Möbius function

An arithmetic function of natural argument: , 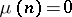if is divisible by the square of a prime number, otherwise , where is the number of prime factors of the number . This function was introduced by A. Möbius in 1832.

The Möbius function is a multiplicative arithmetic function; if 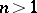. It is used in the study of other arithmetic functions; it appears in inversion formulas (see, e.g. Möbius series). The following estimate is known for the mean value of the Möbius function [2]:

where is a constant. The fact that the mean value tends to zero as 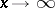implies an asymptotic law for the distribution of prime numbers in the natural series.

The Möbius function is related to the Riemann zeros via the formula

\begin{equation} \sum_{n=1}^{\infty}\frac{\mu(n)}{\sqrt{n}} g \log n = \sum_t \frac{h(t)}{\zeta'(1/2+it)}+2\sum_{n=1}^\infty \frac{ (-1)^{n} (2\pi )^{2n}}{(2n)! \zeta(2n+1)}\int_{-\infty}^{\infty}g(x) e^{-x(2n+1/2)} \, dx,\end{equation}

Here g(x) and h(x) form a Fourier transform pair.

References

[1]	I.M. Vinogradov, "Elements of number theory" , Dover, reprint (1954) (Translated from Russian)
[2]	A. Walfisz, "Weylsche Exponentialsummen in der neueren Zahlentheorie" , Deutsch. Verlag Wissenschaft. (1963)

Comments

The multiplicative arithmetic functions form a group under the convolution product 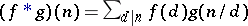. The Möbius function is in fact the inverse of the constant multiplicative function 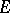(defined by 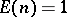for all ) under this convolution product. From this there follows many "inversion formulas" , cf. e.g. Möbius series.

References

[a1]	G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Clarendon Press (1979)