Predicate
A function whose values are statements about  -tuples of objects forming the values of its arguments. For
-tuples of objects forming the values of its arguments. For  a predicate is called a "property" , for
a predicate is called a "property" , for 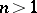 a "relation" ; propositions (cf. Proposition) may be regarded as zero-place predicates.
a "relation" ; propositions (cf. Proposition) may be regarded as zero-place predicates.
In order to specify an  -place predicate
-place predicate 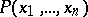 one must indicate sets
one must indicate sets 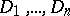 — the domains of variation of the object variables
— the domains of variation of the object variables  ; most often one considers the case
; most often one considers the case 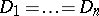 . From the set-theoretical point of view a predicate is specified by a subset
. From the set-theoretical point of view a predicate is specified by a subset  of the Cartesian product
of the Cartesian product 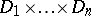 . Here
. Here 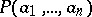 is taken to mean "the ordered tuple a1…an belongs to M" . The syntactic specification of an
is taken to mean "the ordered tuple a1…an belongs to M" . The syntactic specification of an  -place predicate is realized by exhibiting a formula of a logico-mathematical language containing
-place predicate is realized by exhibiting a formula of a logico-mathematical language containing  free variables. The notion of a predicate dates back to Aristotle; the apparatus for operating with statements containing predicates is developed in mathematical logic (cf. Logical calculus; Predicate calculus).
free variables. The notion of a predicate dates back to Aristotle; the apparatus for operating with statements containing predicates is developed in mathematical logic (cf. Logical calculus; Predicate calculus).
Comments
References
| [a1] | S.C. Kleene, "Introduction to metamathematics" , North-Holland (1952) pp. Chapt. XIV |
| [a2] | P. Suppes, "Introduction to logic" , v. Nostrand (1957) pp. §9.8 |
| [a3] | A. Grzegorczyk, "An outline of mathematical logic" , Reidel (1974) |
Predicate. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Predicate&oldid=29767