Strong solution

of a differential equation

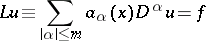in a domain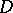

A locally integrable function that has locally integrable generalized derivatives of all orders (cf. Generalized derivative), and satisfies

almost-everywhere in .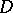

The notion of a "strong solution" can also be introduced as follows. A function is called a strong solution of

if there are sequences of smooth (for example, ) functions 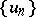, 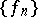such that 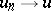, 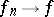and 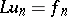for each , where the convergence is taken in 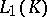for any compact set 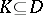. In these definitions, 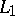can be replaced by the class 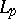of functions whose 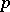-th powers are locally integrable. The class most often used is .

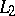In the case of an elliptic equation

both notions of a strong solution coincide.

References

[a1]	J. Chazarain, A. Piriou, "Introduction à la théorie des équations aux dérivées partielles linéaires" , Gauthier-Villars (1981) pp. 223 MR0598467 Zbl 0446.35001