Elliptic partial differential equation

at a given point

A partial differential equation of order ,

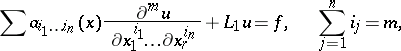such that is a differential operator of order less than , whose characteristic equation at ,

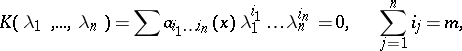has no real roots except .

For second-order equations the characteristic form is quadratic,

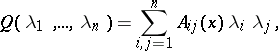and can be brought to the form

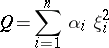by a non-singular affine transformation of the variables , .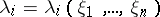

When all or all 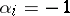, the equation is said to be of elliptic type.

A partial differential equation is said to be of elliptic type in its domain of definition if it is elliptic at every point of this domain.

An elliptic partial differential is called uniformly elliptic if there are positive numbers and such that

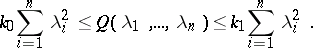For references see Differential equation, partial.

References

[a1]	L.V. Hörmander, "The analysis of linear partial differential operators" , 1 , Springer (1983) MR0717035 MR0705278 Zbl 0521.35002 Zbl 0521.35001